题目内容
18．已知实数x，y满足：y=$\sqrt{x-2}$+$\sqrt{2-x}$+6，求$\sqrt{xy}$-$\sqrt{\frac{y}{x}}$+$\sqrt{3y}$的值．分析 依据二次根式的被开放数不为零可得到x=2，y=6，然后再代入所求的代数式进行计算即可．
解答 解：∵y=$\sqrt{x-2}$+$\sqrt{2-x}$+6有意义，
∴x-2≥0且2-x≥0，
∴x=2．
∴y=6．
∴原式=$\sqrt{12}$+$\sqrt{3}$+$\sqrt{18}$=2$\sqrt{3}$+$\sqrt{3}$+3$\sqrt{2}$=3$\sqrt{3}$+3$\sqrt{2}$．
点评 本题主要考查的是二次根式有意义的条件，由二次根式的被开放数为非负数求得x、y的值是解题的关键．
练习册系列答案
相关题目
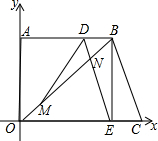如图，在直角梯形OABC中，已知B、C两点的坐标分别为B（8，6）、C（10，0），动点M由原点O出发沿OB方向匀速运动，速度为1单位/秒；同时，线段DE由BC出发沿BA方向匀速运动，速度为1单位/秒，交OB于点N，连接DM，设运动时间为t秒（0＜t＜8）