题目内容
10.(1)计算:$\left\{\begin{array}{l}{2x+y=3}\\{x-y=0}\end{array}\right.$;(2)$\left\{\begin{array}{l}{\frac{x}{3}-\frac{y}{2}=1}\\{3x+2y=22}\end{array}\right.$;
(3)$\left\{\begin{array}{l}{\frac{2(x-y)}{3}-\frac{x+y}{4}=-\frac{1}{12}}\\{3(x+y)-2(2x-y)=3}\end{array}\right.$.
分析 (1)方程组利用加减消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可;
(3)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{2x+y=3①}\\{x-y=0②}\end{array}\right.$,
①+②得:3x=3,即x=1,
把x=1代入②得:y=1,
则方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$;
(2)方程组整理得:$\left\{\begin{array}{l}{2x-3y=6①}\\{3x+2y=22②}\end{array}\right.$,
①×2+②×3得:13x=78,即x=6,
把x=6代入①得:y=2,
则方程组的解为$\left\{\begin{array}{l}{x=6}\\{y=2}\end{array}\right.$;
(3)方程组整理得:$\left\{\begin{array}{l}{5x-11y=-1①}\\{-x+5y=3②}\end{array}\right.$,
①+②×5得:14y=14,即y=1,
把y=1代入②得:x=2,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
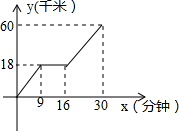 如图,是某汽车行驶的路程y(千米)与时间x(分钟)的函数关系图象,观察图中所提供的信息,解答下列问题.
如图,是某汽车行驶的路程y(千米)与时间x(分钟)的函数关系图象,观察图中所提供的信息,解答下列问题. 画出△ABC关于直线L的对称图形△A′B′C′.
画出△ABC关于直线L的对称图形△A′B′C′. 如图所示,四边形OABC是矩形,点A、C的坐标分别为(6,0),(0,2),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=-x+b交折线OAB于点E.
如图所示,四边形OABC是矩形,点A、C的坐标分别为(6,0),(0,2),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=-x+b交折线OAB于点E.