题目内容
9．先化简再求值：$\frac{{x}^{2}-2x+1}{{x}^{2}-4}$÷（$\frac{1}{x-2}$+1），其中x满足x2+（tan60°-2）x-2$\sqrt{3}$=0．分析 先算括号里面的，再算除法，最后求出x的值代入进行计算即可．
解答 解：原式=$\frac{（x-1）^{2}}{（x+2）（x-2）}$÷$\frac{x-1}{x-2}$
=$\frac{（x-1）^{2}}{（x+2）（x-2）}$•$\frac{x-2}{x-1}$
=$\frac{x-1}{x+2}$．
∵x满足x2+（tan60°-2）x-2$\sqrt{3}$=0，即x2+（$\sqrt{3}$-2）x-2$\sqrt{3}$=0，
∴（x+$\sqrt{3}$）（x-2）=0，
∴x1=-$\sqrt{3}$，x2=2，
当x=-$\sqrt{3}$时，原式=$\frac{-\sqrt{3}-1}{-\sqrt{3}+2}$=-3$\sqrt{3}$-5．
点评 本题考查的是分式的化简求值，此类题型的特点是：利用方程解的定义找到相等关系，再把所求的代数式化简后整理出所找到的相等关系的形式，再把此相等关系整体代入所求代数式，即可求出代数式的值．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC（顶点是网格线的交点）．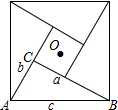
在Rt△ABC中，∠ACB=90°，BC=a，AC=b．AB=c，将Rt△ABC绕点O依次旋转90°、180°和270°，构成的图形如图所示，该图是我国古代数学家赵爽制作的“勾股圆方图”，也被称作“赵爽弦图”，它是我国最早对勾股定理证明的记载，也成为了2002年在北京召开的国际数学家大会的会标设计的主要依据．