题目内容
5.某地计划用80-120天(含80与120天)的时间建设一项水利工程,工程需要运送的土石方总量为360万米3.(1)写出运输公司完成任务所需的时间y(单位:天)与平均每天的工作量x(单位:万米3)之间的函数关系式,并给出自变量x的取值范围;
(2)由于工程进度的需要,实际运送土石方总量比原计划多400000米3,工期比原计划多用了10天,则平均每天运送土石方数是多少万米3?
分析 (1)根据题意可以写出运输公司完成任务所需的时间y(单位:天)与平均每天的工作量x(单位:万米3)之间的函数关系式,然后根据计划用80-120天(含80与120天)的时间建设一项水利工程,可以求得x的取值范围;
(2)根据题意可以列出相应的分式方程,本题得以解决.
解答 解:(1)由题意可得,
y=$\frac{360}{x}$,
∵计划用80-120天(含80与120天)的时间建设一项水利工程,
∴当80≤$\frac{360}{x}$≤120,
得3≤x≤4.5,
即运输公司完成任务所需的时间y(单位:天)与平均每天的工作量x(单位:万米3)之间的函数关系式是y=$\frac{360}{x}$(3≤x≤4.5);
(2)设平均每天运送土石方数是x万米3,
$\frac{360+40}{x}-\frac{360}{x}=10$,
解得,x=4,
经检验x=4是原分式方程的解,
即平均每天运送土石方数是4万米3.
点评 本题考查分式方程的应用、反比例函数的应用,解答此类问题的关键是明确题意,找出所求问题需要的条件,利用函数和方程的相关知识解答.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
20.在△ABC中,AB=AC=4,∠B=30°,点P是线段BC上一动点,则线段AP的长可能是( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
 如图,点O是直线EP上一点,射线OA,OB,OC在直线EF的上方,射线OD在直线EF的下方,且OF平分∠COD,OA⊥OC,OB⊥OD.
如图,点O是直线EP上一点,射线OA,OB,OC在直线EF的上方,射线OD在直线EF的下方,且OF平分∠COD,OA⊥OC,OB⊥OD.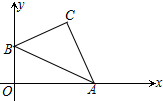 在平面直角坐标系中,已知点A、B的坐标分别为A(6,0)、B(0,2),以AB为斜边在右上方作Rt△ABC.设点C坐标为(x,y),则(x+y)的最大值=4+2$\sqrt{5}$.
在平面直角坐标系中,已知点A、B的坐标分别为A(6,0)、B(0,2),以AB为斜边在右上方作Rt△ABC.设点C坐标为(x,y),则(x+y)的最大值=4+2$\sqrt{5}$.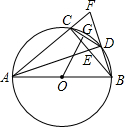 如图,⊙O是Rt△ABC的外接圆,AC=BC,∠CAB的平分线AD交BC于点E、交⊙O于点D,延长BD交AC的延长线线于点F,连结CD、OG平分CD.
如图,⊙O是Rt△ABC的外接圆,AC=BC,∠CAB的平分线AD交BC于点E、交⊙O于点D,延长BD交AC的延长线线于点F,连结CD、OG平分CD. 甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,甲出发1h后,乙出发,两人到达B地后立刻按原速度返回,设甲与A地相距y甲(km),乙与A地相距y乙(km),甲离开A地的时间为x(h),y甲、y乙与x之间的函数图象如图所示.
甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,甲出发1h后,乙出发,两人到达B地后立刻按原速度返回,设甲与A地相距y甲(km),乙与A地相距y乙(km),甲离开A地的时间为x(h),y甲、y乙与x之间的函数图象如图所示.