题目内容
8. 如图,点O是直线EP上一点,射线OA,OB,OC在直线EF的上方,射线OD在直线EF的下方,且OF平分∠COD,OA⊥OC,OB⊥OD.
如图,点O是直线EP上一点,射线OA,OB,OC在直线EF的上方,射线OD在直线EF的下方,且OF平分∠COD,OA⊥OC,OB⊥OD.(1)若∠DOF=30°,求∠AOB的度数;
(2)若OA平分∠BOE,则∠DOF的度数是30°(直接写出答案)
分析 (1)利用角平分线定理得到∠COD=2∠DOF=60°,再利用垂直定义得到∠BOD=90°,则∠BOC=30°,接着由OA⊥OC得到∠AOC=90°,然后利用互余计算∠AOB的度数;
(2)由角平分线定义得到∠AOB=∠AOE,再利用等角的余角相等得到∠BOC=∠COF,加上∠COF=∠DOF,于是得到∠DOF=$\frac{1}{3}$∠BOD=30°.
解答 解:(1)∵OF平分∠COD,
∴∠COD=2∠DOF=60°,
∵OB⊥OD,
∴∠BOD=90°,
∴∠BOC=90°-60°=30°,
∵OA⊥OC,
∴∠AOC=90°,
∴∠AOB=90°-30°=60°;
(2)∵OA平分∠BOE,
∴∠AOB=∠AOE,
∵OA⊥OC,
∴∠AOC=90°,
∴∠BOC=90°-∠AOB,∠COF=90°-∠AOE,
∴∠BOC=∠COF,
∵OF平分∠COD,
∴∠COF=∠DOF,
∴∠DOF=$\frac{1}{3}$∠BOD=$\frac{1}{3}$×90°=30°.
故答案为30°.
点评 本题考查了垂线:当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直.也考查了角平分线的定义和邻补角.

练习册系列答案
相关题目
 如图,△ABC中,AC=8cm,BC=6cm,AB=10cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2cm,设运动的时间为t秒.
如图,△ABC中,AC=8cm,BC=6cm,AB=10cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2cm,设运动的时间为t秒.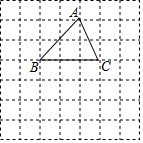 如图,在正方形网格中,△ABC的顶点C的坐标为(2,1).
如图,在正方形网格中,△ABC的顶点C的坐标为(2,1).