题目内容
5.△ABC中,AB=AC,D是AB的中点,E,F是AC上的动点,EF=$\frac{1}{2}$AC.(1)若BF⊥AC,求证:CF•CA=$\frac{1}{2}$BC2;
(2)若BF⊥AC,tan∠CBF=$\frac{1}{3}$,求$\frac{DE}{EF}$的值;
(3)ED,FB的延长线交于点G,GH∥BC交AC的延长线于H,求证:EF=FH
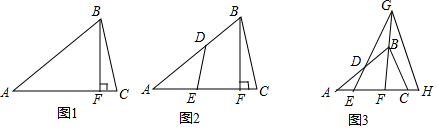
分析 (1)如图1中,作AH⊥BC于H,HN⊥AC于N.只要证明△HCN∽△ACH,可得$\frac{CH}{AC}$=$\frac{CN}{CH}$,推出CH2=CN•CA,再证明CH=$\frac{1}{2}$BC,CN=$\frac{1}{2}$CF,代入即可解决问题;
(2)如图2中,作DH⊥AC于H,设CF=a.在Rt△DEH中,求出DE(用a的代数式表示)即可解决问题;
(3)如图3中,作BM∥AC交EG于M,取AC中点N,连接DN,NM.首先证明四边形MNFB是平行四边形,推出MN=BF,MN∥FG,推出$\frac{EN}{EF}$=$\frac{MN}{FG}$=$\frac{BF}{FG}$,由BC∥GH,推出$\frac{BF}{FG}$=$\frac{FC}{FH}$,推出$\frac{EN}{EF}$=$\frac{FC}{FH}$,再证明EN=CF,即可解决问题;
解答 (1)证明:如图1中,作AH⊥BC于H,HN⊥AC于N.
∵AB=AC,AH⊥BC,
∴BH=CH,∠AHC=∠HNC=90°,
∵∠HCN=∠GCA,
∴△HCN∽△ACH,
∴$\frac{CH}{AC}$=$\frac{CN}{CH}$,
∴CH2=CN•CA,
∵HN∥BF,HB=HC,
∴NC=FN,
∴CH=$\frac{1}{2}$BC,CN=$\frac{1}{2}$CF,
∴($\frac{1}{2}$BC)2=$\frac{1}{2}$•CF•AC,
∴CF•CA=$\frac{1}{2}$BC2.
(2)解:如图2中,作DH⊥AC于H,设CF=a.
在Rt△BCF中,∵tan∠CBF=$\frac{1}{3}$,CF=a,
∴$\frac{CF}{BF}$=$\frac{1}{3}$,BF=3a,
BC2=CF2+BF2=10a2,
∵∴CF•CA=$\frac{1}{2}$BC2,
∴AC=5a,
∴AB=AC=5a,AF=4a,
∵AD=DB,DH∥BF,
∴AH=HF=2a,
∵EF=$\frac{1}{2}$AC=$\frac{5}{2}$a,
∴DH=$\frac{1}{2}$BF=$\frac{3}{2}$a,EH=$\frac{1}{2}$a,
在Rt△DEH中,DE=$\sqrt{E{H}^{2}+D{H}^{2}}$=$\sqrt{(\frac{1}{2}a)^{2}+(\frac{3}{2}a)^{2}}$=$\frac{\sqrt{10}}{2}$a,
∴$\frac{DE}{EF}$=$\frac{\frac{\sqrt{10}}{2}a}{\frac{5}{2}a}$=$\frac{\sqrt{10}}{5}$.
(3)证明:如图3中,作BM∥AC交EG于M,取AC中点N,连接DN,NM.
∵AD=DB,∠ADE=∠MDB,∠A=∠MBD,
∴△ADE≌△BDM,
∴AE=BM,
∵EF=AN=$\frac{1}{2}$AC,
∴AE=FN,
∴BM=FN,BM∥FN,
∴四边形MNFB是平行四边形,MN=BF,
∴MN∥FG,
∴$\frac{EN}{EF}$=$\frac{MN}{FG}$=$\frac{BF}{FG}$,
∵BC∥GH,
∴$\frac{BF}{FG}$=$\frac{FC}{FH}$,
∴$\frac{EN}{EF}$=$\frac{FC}{FH}$,
∵EF=NC,
∴EN=CF,
∴EF=FH.
点评 本题考查三角形综合题、相似三角形的判定和性质、平行线的性质、平行四边形的判定和性质、三角形的中位线定理、勾股定理等知识,解题的关键是学会添加常用辅助线,构造相似三角形解决问题,学会利用参数解决问题,属于中考压轴题.

 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案| A. | (a+0.5)(a-0.5) | B. | (x+y)(-x-y) | C. | (3a+4b)(3b-4a) | D. | (a2+b2)(a2+b2) |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,这是一个“上”字的造型,其中AB∥CD,∠DCE=80°,则∠BEF等于( )
如图,这是一个“上”字的造型,其中AB∥CD,∠DCE=80°,则∠BEF等于( )| A. | 100° | B. | 90° | C. | 80° | D. | 70° |
 请按要求画出函数y=$\frac{1}{2}$x2的图象:
请按要求画出函数y=$\frac{1}{2}$x2的图象:(1)列表;
| x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y | … | $\frac{9}{2}$ | 2 | $\frac{1}{2}$ | 0 | $\frac{1}{2}$ | 2 | $\frac{9}{2}$ | … |
(3)连线;
(4)请你判断点(4,8)、(-$\frac{1}{2}$,-$\frac{1}{8}$)是否在函数图象上,答:点(4,8)在函数图象上,点(-$\frac{1}{2}$,-$\frac{1}{8}$)不在函数图象上.
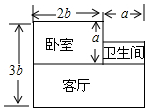 小张刚搬进一套新房子,如图所示(单位:m),他打算把客厅铺上地砖
小张刚搬进一套新房子,如图所示(单位:m),他打算把客厅铺上地砖 如图,网格中每个小正方形的边长都为1,A、B、C都在格点上,试问△ABC是直角三角形吗?请说明理由.
如图,网格中每个小正方形的边长都为1,A、B、C都在格点上,试问△ABC是直角三角形吗?请说明理由.