题目内容
20.过点(-1,7)的直线l与x轴,y轴分别相交于点A,B,且与直线y=-$\frac{4}{3}$x+1平行.(1)求直线l的解析式;
(2)写出在线段AB上,横、纵坐标都是整数的点的坐标.
分析 (1)利用两直线平行的问题可设直线l的解析式为y=-$\frac{4}{3}$x+b,然后把(-1,7)代入求出b,即可得到直线l的解析式;
(2)先确定A和B的坐标,则可得到线段AB上点的横坐标的取值范围为0<x<$\frac{17}{4}$,所以整数x为1,2,3,4,然后根据一次函数图象上点的坐标特征分别计算出对应的函数值,于是可得到在线段AB上,横、纵坐标都是整数的点的坐标.
解答 解:(1)∵过点(-1,7)的一条直线与直线y=-$\frac{4}{3}$x+1平行,
∴设直线l的解析式为y=-$\frac{4}{3}$x+b,
把(-1,7)代入得$\frac{4}{3}$x+b=7,解得b=$\frac{17}{3}$,
∴直线l的解析式为y=-$\frac{4}{3}$x+$\frac{17}{3}$;
(2)当y=0,-$\frac{4}{3}$x+$\frac{17}{3}$=0,解得x=$\frac{17}{4}$,则A($\frac{17}{4}$,0),
当x=0,y=-$\frac{4}{3}$x+$\frac{17}{3}$=$\frac{17}{3}$,则B(0,$\frac{17}{3}$),
∴0<x<$\frac{17}{4}$,
∴整数x为1,2,3,4,
当x=1时,y=-$\frac{4}{3}$x+$\frac{17}{3}$=$\frac{13}{3}$,
当x=2时,y=-$\frac{4}{3}$x+$\frac{17}{3}$=3,
当x=3时,y=-$\frac{4}{3}$x+$\frac{17}{3}$=$\frac{5}{3}$,
当x=4时,y=-$\frac{4}{3}$x+$\frac{17}{3}$=$\frac{1}{3}$,
∴在线段AB上,横、纵坐标都是整数的点的坐标是(2,3).
点评 本题考查了两直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.也考查了一次函数图象上点的坐标特征.

 名校课堂系列答案
名校课堂系列答案| 甲 | 9 | 8 | 10 | 6 | 9 |
| 乙 | 8 | 7 | 8 | 9 | 10 |
(2)指出乙队成绩的众数;
(3)若计算出方差为:S${\;}_{甲}^{2}$=1.84,S${\;}_{乙}^{2}$=1.04,判断哪队的成绩更整齐?
| 班级 | 参加人数 | 中位数 |
| 甲 | 56 | 149 |
| 乙 | 56 | 151 |
| A. | 甲比乙高 | B. | 乙比甲高 | C. | 甲不比乙高 | D. | 乙不比甲高 |
| A. | 10和8 | B. | 10和9 | C. | 9和8 | D. | 8和8 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
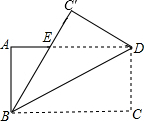 如图,将矩形ABCD沿对角线BD折叠,使点C与C′重合.若AB=3,则C′D的长为3.
如图,将矩形ABCD沿对角线BD折叠,使点C与C′重合.若AB=3,则C′D的长为3.