题目内容
14.下列事件:①两直线平行,同位角相等;②掷一枚硬币,国徽的一面朝上,其中,随机事件是②.(填序号)分析 根据平行线的性质和事件发生的可能性大小判断相应事件的类型即可.
解答 解:①两直线平行,同位角相等是必然事件;
②掷一枚硬币,国徽的一面朝上是随机事件,
故答案为:②.
点评 本题考查的是必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.

练习册系列答案
相关题目
4.求1+2+22+23+…+22016的值,可令S=1+2+22+23+…+22016,则2S=2+22+23+…+22016+22017,因此2S-S=22017-1,S=22017-1.参照以上推理,计算5+52+53+…+52016的值为( )
| A. | 52017-1 | B. | 52017-5 | C. | $\frac{{{5^{2017}}-1}}{4}$ | D. | $\frac{{{5^{2017}}-5}}{4}$ |
2. 如图,9点整时,时针与分针夹角为90°,则下一次时针与分针夹角为90°时,经过了( )分钟.
如图,9点整时,时针与分针夹角为90°,则下一次时针与分针夹角为90°时,经过了( )分钟.
 如图,9点整时,时针与分针夹角为90°,则下一次时针与分针夹角为90°时,经过了( )分钟.
如图,9点整时,时针与分针夹角为90°,则下一次时针与分针夹角为90°时,经过了( )分钟.| A. | $\frac{90}{11}$ | B. | $\frac{180}{11}$ | C. | $\frac{270}{11}$ | D. | $\frac{360}{11}$ |
9.若3×9m×27m=316,则m的值是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
3.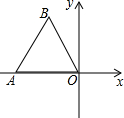 如图,点O为平面直角坐标系的原点,点A在x轴上,△OAB是边长为4的等边三角形,以O为旋转中心,将△OAB按顺时针方向旋转60°,得到△OA′B′,那么点A′的坐标为( )
如图,点O为平面直角坐标系的原点,点A在x轴上,△OAB是边长为4的等边三角形,以O为旋转中心,将△OAB按顺时针方向旋转60°,得到△OA′B′,那么点A′的坐标为( )
 如图,点O为平面直角坐标系的原点,点A在x轴上,△OAB是边长为4的等边三角形,以O为旋转中心,将△OAB按顺时针方向旋转60°,得到△OA′B′,那么点A′的坐标为( )
如图,点O为平面直角坐标系的原点,点A在x轴上,△OAB是边长为4的等边三角形,以O为旋转中心,将△OAB按顺时针方向旋转60°,得到△OA′B′,那么点A′的坐标为( )| A. | (2,2$\sqrt{3}$) | B. | (-2,4) | C. | (-2,2$\sqrt{2}$) | D. | (-2,2$\sqrt{3}$) |
4.函数y=$\frac{\sqrt{x+1}}{{x}^{2}-4}$的自变量x的取值范围是( )
| A. | x≥-1 | B. | x≥-1且x≠2 | C. | x≠±2 | D. | x>-1且x≠2 |
 如图,在一个足够大的桌面上,画满了等距的平行线,间距为2厘米,现有一个半径为r厘米的圆形硬币,若事件“将该硬币任意掷于桌面上,硬币压到所画直线”是必然事件,则r的取值可以是2.
如图,在一个足够大的桌面上,画满了等距的平行线,间距为2厘米,现有一个半径为r厘米的圆形硬币,若事件“将该硬币任意掷于桌面上,硬币压到所画直线”是必然事件,则r的取值可以是2.