题目内容
如图所示，△ABC中，中线BD、CE相交于O，F、G分别为OB、OC的中点．判断四边形DEFG的形状并进行证明．考点：中点四边形
专题：
分析：利用三角形中位线定理得出FG=DE，且FG∥DE，进而得出四边形DEFG的形状．
解答：解：四边形DEFG是平行四边形，
理由：∵中线BD、CE，
∴DE=
BC，且DE∥BC，
又∵F、G分别是OB、OC的中点，
∴FG=
BC，且FG∥BC，
∴FG=DE，且FG∥DE．
∴四边形DEFG是平行四边形．
理由：∵中线BD、CE，
∴DE=
| 1 |
| 2 |
又∵F、G分别是OB、OC的中点，
∴FG=
| 1 |
| 2 |
∴FG=DE，且FG∥DE．
∴四边形DEFG是平行四边形．
点评：此题主要考查了中点四边形，正确利用三角形中位线定理是解题关键．
练习册系列答案
相关题目
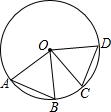已知，如图，∠AOB=∠COD，下列结论不一定成立的是（ ）| A、AB=CD | ||||
B、
| ||||
| C、△AOB≌△COD | ||||
| D、△AOB、△COD都是等边三角形 |
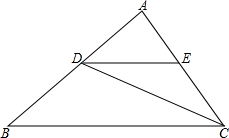如图，点D、E分别在△ABC的边AB、AC上，AD=4，BD=5，DE∥BC，∠ACD=∠B．
如图，在矩形ABCD中，对角线AC、BD相交于点O，点E、F分别是AO、AD的中点，若AB=6cm，BC=8cm，求△AEF的周长．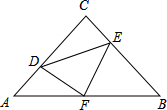
如图，在等腰Rt△ABC中，∠C=90°，AC=6，F是AB边上的中点，点D、E分别在AC、BC边上运动，连结DE、DF、EF，且保持DF⊥EF，在此运动变化的过程中，当△ADF与△BEF的面积为1：2，则DE的长为