题目内容
15. 我市某中学举行“中国梦•校园好声音”歌手大赛,初、高中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩(满分为100分)如图所示.(方差公式:s2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2])
我市某中学举行“中国梦•校园好声音”歌手大赛,初、高中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩(满分为100分)如图所示.(方差公式:s2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2])(1)根据图示填写表格单位(分);
| 平均数/分 | 中位数/分 | 众数/分 | |
| 初中代表队 | 85 | 85 | 85 |
| 高中代表队 | 85 | 80 | 100 |
(3)计算两队决赛成绩的方差判断哪一个代表队选手成绩较为稳定.
分析 (1)根据平均数的计算公式和众数、中位数的定义分别进行解答,然后把表补充完整即可;
(2)根据平均数相同的情况下,中位数高的哪个队的决赛成绩较好;
(3)根据方差公式先算出各队的方差,然后根据方差的意义即可得出答案.
解答 解:(1)初中代表队的平均成绩是:(75+80+85+85+100)÷5=85(分),
在初中代表队中85出现了2次,出现的次数最多,则众数是85分;
把高中代表队的成绩从小到大排列为:70,75,80,100,100,最中间的数是80,则中位数是80分;
填表如下:
| 平均数/分 | 中位数/分 | 众数/分 | |
| 初中代表队 | 85 | 85 | 85 |
| 高中代表队 | 85 | 80 | 100 |
(2)初中部成绩好些,因为两个队的平均数都相同,初中部的中位数高,
所以在平均数相同的情况下,中位数高的初中部成绩好些;
(3)初中代表队的方差是:$\frac{1}{5}$[(75-85)2+(80-85)2+(85-85)2+(85-85)2+(100-85)2]=70,
高中代表队的方差是:$\frac{1}{5}$[(70-85)2+(75-85)2+(80-85)2+(100-85)2+(100-85)2]=160,
∵S初中2<S高中2,
∴初中代表队选手成绩较稳定.
点评 本题考查方差的定义:一般地设n个数据,x1,x2,…xn的平均数为$\overline{x}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.

练习册系列答案
相关题目
4.对于抛物线y=-$\frac{1}{2}$(x-1)2+3,下列说法正确的是( )
| A. | 开口向下,顶点坐标(1,3) | B. | 开口向上,顶点坐标(3,-1) | ||
| C. | 开口向下,顶点坐标(-1,3) | D. | 开口向上,顶点坐标(-3,1) |
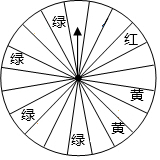 某商场为了吸引顾客,设立了一个可以自由转动的转盘(转盘被等分成20个扇形,如图)并规定:顾客在本商场每消费200元,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准红、黄或绿色区域,顾客就可以分别获得100元、50元、20元的购物券.某顾客消费210元,他转动转盘获得购物券的概率是多少?他得到100元、50元、20元购物券的概率分别是多少?
某商场为了吸引顾客,设立了一个可以自由转动的转盘(转盘被等分成20个扇形,如图)并规定:顾客在本商场每消费200元,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准红、黄或绿色区域,顾客就可以分别获得100元、50元、20元的购物券.某顾客消费210元,他转动转盘获得购物券的概率是多少?他得到100元、50元、20元购物券的概率分别是多少? 如图,在平行四边形ABCD中,E,F分别是AB,CD边上的点,且AE=CF,求证:四边形EBFD是平行四边形.
如图,在平行四边形ABCD中,E,F分别是AB,CD边上的点,且AE=CF,求证:四边形EBFD是平行四边形.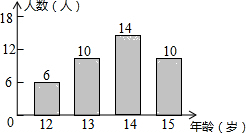 某校共有40名初中生参加足球兴趣小组,他们的年龄统计情况如图所示,则这40名学生年龄的中位数是14岁.
某校共有40名初中生参加足球兴趣小组,他们的年龄统计情况如图所示,则这40名学生年龄的中位数是14岁.