题目内容
(1)抛物线m1:y1=a1x2+b1x+c1中,函数y1与自变量x之间的部分对应值如表:
| x | … | ﹣2 | ﹣1 | 1 | 2 | 4 | 5 | … |
| y1 | … | ﹣5 | 0 | 4 | 3 | ﹣5 | ﹣12 | … |
设抛物线m1的顶点为P,与y轴的交点为C,则点P的坐标为 ,点C的坐标为 .
(2)将设抛物线m1沿x轴翻折,得到抛物线m2:y2=a2x2+b2x+c2,则当x=﹣3时,y2= .
(3)在(1)的条件下,将抛物线m1沿水平方向平移,得到抛物线m3.设抛物线m1与x轴交于A,B两点(点A在点B的左侧),抛物线m3与x轴交于M,N两点(点M在点N的左侧).过点C作平行于x轴的直线,交抛物线m3于点K.问:是否存在以A,C,K,M为顶点的四边形是菱形的情形?若存在,请求出点K的坐标;若不存在,请说明理由.
【考点】二次函数综合题.
【专题】综合题.
【分析】(1)先利用待定系数法求出抛物线m1的解析式为y1=﹣x2+2x+3,再配成顶点式可得到P点坐标,然后计算自变量为0时的函数值即可得到C点坐标;
(2)根据抛物线的几何变换得到抛物线m1与抛物线m2的二次项系数互为相反数,然后利用顶点式写出抛物线m2的解析式,再计算自变量为﹣3时的函数值;
(3)先确定A点坐标,再根据平移的性质得到四边形AMKC为平行四边形,根据菱形的判定方法,当CA=CK时,四边形AMKC为菱形,接着计算出AC=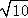 ,则CK=
,则CK=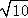 ,然后根据平移的方向不同得到K点坐标.
,然后根据平移的方向不同得到K点坐标.
【解答】解:(1)把(﹣1,0),(1,4),(2,3)分别代入y1=a1x2+b1x+c1得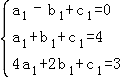 ,
,
解得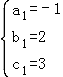 .
.
所以抛物线m1的解析式为y1=﹣x2+2x+3=﹣(x﹣1)2+4,则P(1,4),
当x=0时,y=3,则C(0,3);
(2)因为抛物线m1沿x轴翻折,得到抛物线m2,
所以y2=(x﹣1)2﹣4,当x=﹣3时,y2=(x+1)2﹣4=(﹣3﹣1)2﹣4=12.
故答案为(1,4),(0,3),12;
(3)存在.
当y1=0时,﹣x2+2x+3=0,解得x1=﹣1,x2=3,则A(﹣1,0),B(3,0),
∵抛物线m1沿水平方向平移,得到抛物线m3,
∴CK∥AM,CK=AM,
∴四边形AMKC为平行四边形,
当CA=CK时,四边形AMKC为菱形,而AC=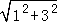 =
=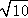 ,则CK=
,则CK=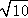 ,
,
当抛物线m1沿水平方向向右平移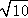 个单位,此时K(
个单位,此时K(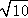 ,3);当抛物线m1沿水平方向向左平移
,3);当抛物线m1沿水平方向向左平移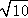 个单位,此时K(﹣
个单位,此时K(﹣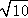 ,3).
,3).
【点评】本题考查了二次函数的综合题:熟练掌握二次函数的性质和菱形的判定;会利用待定系数法求二次函数解析式;会运用数形结合的数学思想方法解决问题.

 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案