题目内容
甲乙两人分别从距目的地6千米和10千米的两地同时出发,甲乙的速度比是3:4,结果甲比乙提前20分钟到达目的地,求甲、乙两人的速度.
【考点】分式方程的应用.
【专题】应用题.
【分析】求的是速度,路程明显,一定是根据时间来列等量关系,本题的关键描述语是:甲比乙提前20分钟到达目的地.等量关系为:甲走6千米用的时间+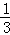 =乙走10千米用的时间.
=乙走10千米用的时间.
【解答】解:设甲的速度为3x千米/时,则乙的速度为4x千米/时.
根据题意,得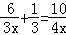 ,
,
解得x=1.5.
经检验,x=1.5是原方程的根.
所以甲的速度为3x=4.5千米/时,乙的速度为4x=6千米/时.
答:甲的速度为4.5千米/时,乙的速度为6千米/时.
【点评】本题考查分式方程的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.当题中出现比值问题时,应设比中的每一份为x.

练习册系列答案
相关题目
(1)抛物线m1:y1=a1x2+b1x+c1中,函数y1与自变量x之间的部分对应值如表:
| x | … | ﹣2 | ﹣1 | 1 | 2 | 4 | 5 | … |
| y1 | … | ﹣5 | 0 | 4 | 3 | ﹣5 | ﹣12 | … |
设抛物线m1的顶点为P,与y轴的交点为C,则点P的坐标为 ,点C的坐标为 .
(2)将设抛物线m1沿x轴翻折,得到抛物线m2:y2=a2x2+b2x+c2,则当x=﹣3时,y2= .
(3)在(1)的条件下,将抛物线m1沿水平方向平移,得到抛物线m3.设抛物线m1与x轴交于A,B两点(点A在点B的左侧),抛物线m3与x轴交于M,N两点(点M在点N的左侧).过点C作平行于x轴的直线,交抛物线m3于点K.问:是否存在以A,C,K,M为顶点的四边形是菱形的情形?若存在,请求出点K的坐标;若不存在,请说明理由.
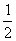 x2的图象向左平移2个单位,在向下平移1个单位,得到的函数表达式为
x2的图象向左平移2个单位,在向下平移1个单位,得到的函数表达式为 ∠ABC,点D为直线BC上的动点,过点D作直线CM的垂线,垂足为E,交直线AC于F.
∠ABC,点D为直线BC上的动点,过点D作直线CM的垂线,垂足为E,交直线AC于F.