题目内容
8.设[x]表示不超过实数x的最大整数.若实数a满足a-$\frac{4}{a}+\frac{3\sqrt{a(a-2)}}{a}=2$,则[a]=( )| A. | 0或2 | B. | -1或2 | C. | 0或3 | D. | -3或2 |
分析 首先将原式化简,进而结合换元法解方程,进而得出a的值,再利用取整计算的性质得出答案.
解答 解:由已知得a2-4+3$\sqrt{a(a-2)}$=2a,
设$\sqrt{a(a-2)}$=x,
则a2-2a=a(a-2)=x2,
故原式可变为:x2+3x-4=0,
解得:x1=1,x2=-4(舍去),
于是,$\sqrt{a(a-2)}$=1,
则a(a-2)=1,
解得:a1=1+$\sqrt{2}$,a2=1-$\sqrt{2}$,
则[a]=-1或2.
故选:B.
点评 此题主要考查了取整计算以及无理方程的解法,正确将原式变形结合换元法求出是解题关键.

练习册系列答案
相关题目
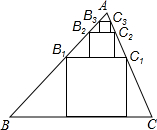 如图,在△ABC中,BC=6,S△ABC=12,B1C1所在四边形是△ABC的内接正方形,B2C2所在四边形是△AB1C1的内接正方形,B3C3所在四边形是△AB2C2的内接正方形,依此类推,则BnCn的长为6×($\frac{2}{5}$)n.
如图,在△ABC中,BC=6,S△ABC=12,B1C1所在四边形是△ABC的内接正方形,B2C2所在四边形是△AB1C1的内接正方形,B3C3所在四边形是△AB2C2的内接正方形,依此类推,则BnCn的长为6×($\frac{2}{5}$)n.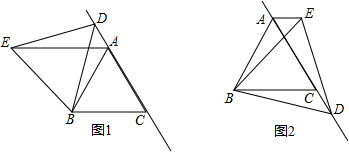
 如图,△ABD、△AEC都是等边三角形,直线CD与直线BE交于点F.
如图,△ABD、△AEC都是等边三角形,直线CD与直线BE交于点F. 一个几何体的正视图与左视图相同,均为如图所示,则其俯视图可能是( )
一个几何体的正视图与左视图相同,均为如图所示,则其俯视图可能是( )


