题目内容
 如图,以?ABCD的边AB为直径的⊙O经过点D,点E在⊙O上,∠AED=45°,
如图,以?ABCD的边AB为直径的⊙O经过点D,点E在⊙O上,∠AED=45°,(1)判断CD与⊙O的关系,并说明理由.
(2)若已知:∠ADE=54°,⊙O的半径为5,求劣弧AE的长.
考点:切线的判定,平行四边形的性质,弧长的计算
专题:计算题
分析:(1)连结OD,根据圆周角定理得到∠AOD=2∠AED=90°,再利用平行四边形的性质得AB∥CD,则∠CDO=∠DOA=90°,所以OD⊥DC,然后根据切线的判定定理得到CD与⊙O相切;
(2)连结OE,根据圆周角定理得到∠AOE=2∠ADE=108°,然后根据弧长公式计算.
(2)连结OE,根据圆周角定理得到∠AOE=2∠ADE=108°,然后根据弧长公式计算.
解答: 解:(1)CD与⊙O相切.理由如下:
解:(1)CD与⊙O相切.理由如下:
连结OD,如图,
∵∠AED=45°,
∴∠AOD=2∠AED=90°,
∵四边形ABCD为平行四边形,
∴AB∥CD,
∴∠CDO=∠DOA=90°,
∴OD⊥DC,
∴CD与⊙O相切;
(2)连结OE,
∵∠AOE=2∠ADE=2×54°=108°,
∴劣弧AE的长=
=3π.
 解:(1)CD与⊙O相切.理由如下:
解:(1)CD与⊙O相切.理由如下:连结OD,如图,
∵∠AED=45°,
∴∠AOD=2∠AED=90°,
∵四边形ABCD为平行四边形,
∴AB∥CD,
∴∠CDO=∠DOA=90°,
∴OD⊥DC,
∴CD与⊙O相切;
(2)连结OE,
∵∠AOE=2∠ADE=2×54°=108°,
∴劣弧AE的长=
| 108•π•5 |
| 180 |
点评:本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了圆周角定理、平行四边形的性质和弧长公式.

练习册系列答案
相关题目
 如图,已知点M、N分别为?ABCD的边CD、AB的中点,连接AM、CN.
如图,已知点M、N分别为?ABCD的边CD、AB的中点,连接AM、CN.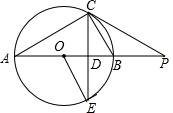 如图,AB是⊙O的直径,弦CE⊥AB交AB于点D,点P在AB的延长线上,连结OE、AC、BC,已知∠POE=2∠PCB.
如图,AB是⊙O的直径,弦CE⊥AB交AB于点D,点P在AB的延长线上,连结OE、AC、BC,已知∠POE=2∠PCB.
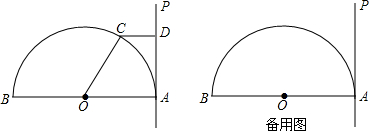
 解不等式组:
解不等式组: 如图,已知二次函数y=x2+bx+c的图象的对称轴为过点(1,0)且与y轴平行的直线,点A、B均在图象上,且直线AB与x轴平行,若点A的坐标为(0,
如图,已知二次函数y=x2+bx+c的图象的对称轴为过点(1,0)且与y轴平行的直线,点A、B均在图象上,且直线AB与x轴平行,若点A的坐标为(0,