题目内容
【问题解决】
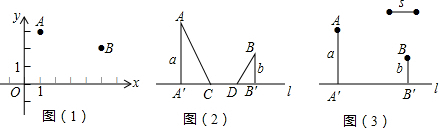
如图(1),已知点A(1,3),B(5,2),在x轴上确定一点P,使AP+BP的值最小.
【问题拓展】
如图(2),河岸l同侧的两个居民小区A、B到河岸的距离分别为a米、b米(即AA′=a米,BB′=b米),A′B′=c米.现欲在河岸边建一个长度为s米的绿化带CD(宽度不计),使C到小区A的距离与D到小区B的距离之和最小(AC+BD最小).
(1)在图(3)中画出绿化带的位置,写出画图过程并说明理由;
(2)求AC+BD的最小值.
如图(1),已知点A(1,3),B(5,2),在x轴上确定一点P,使AP+BP的值最小.
【问题拓展】
如图(2),河岸l同侧的两个居民小区A、B到河岸的距离分别为a米、b米(即AA′=a米,BB′=b米),A′B′=c米.现欲在河岸边建一个长度为s米的绿化带CD(宽度不计),使C到小区A的距离与D到小区B的距离之和最小(AC+BD最小).
(1)在图(3)中画出绿化带的位置,写出画图过程并说明理由;
(2)求AC+BD的最小值.

考点:轴对称-最短路线问题,坐标与图形性质
专题:
分析:【问题解决】作出B关于x轴的对称点E,连接A与对称点E交x轴于P,P即为所求.
【问题拓展】(1)作出B关于x轴的对称点E,过E作EF∥x轴,使EF=S,连接AF交x轴于C,过E作ED∥AF,交x轴于D,则CD即为所求;
(2)根据勾股定理即可求得.
【问题拓展】(1)作出B关于x轴的对称点E,过E作EF∥x轴,使EF=S,连接AF交x轴于C,过E作ED∥AF,交x轴于D,则CD即为所求;
(2)根据勾股定理即可求得.
解答:解:【问题解决】
如图1,作出B关于x轴的对称点E,连接A与对称点E交x轴于P,P即为所求;

【问题拓展】
(1)如图3,作出B关于x轴的对称点E,过E作EF∥x轴,使EF=S,连接AF交x轴于C,过E作ED∥AF,交x轴于D,则CD即为所求;
∵EF∥x轴,ED∥AF,
∴四边形CDEF是平行四边形,
∴EF=CD,CF=DE,
∴AC+BD=AC+CF=AF,
根据两点之间线段最短,所以此时C到小区A的距离与D到小区B的距离之和最小.
(2)AC+BD=AF=
.
如图1,作出B关于x轴的对称点E,连接A与对称点E交x轴于P,P即为所求;

【问题拓展】
(1)如图3,作出B关于x轴的对称点E,过E作EF∥x轴,使EF=S,连接AF交x轴于C,过E作ED∥AF,交x轴于D,则CD即为所求;
∵EF∥x轴,ED∥AF,
∴四边形CDEF是平行四边形,
∴EF=CD,CF=DE,
∴AC+BD=AC+CF=AF,
根据两点之间线段最短,所以此时C到小区A的距离与D到小区B的距离之和最小.
(2)AC+BD=AF=
| (a+b)2+(c-s)2 |
点评:本题考查了轴对称-最短路线问题,坐标与图形的性质,确定出C的位置是本题的关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
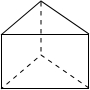 用平面去截如图所示的三棱柱,截面形状不可能是( )
用平面去截如图所示的三棱柱,截面形状不可能是( )| A、三角形 | B、四边形 |
| C、五边形 | D、六边形 |
在数轴上,与表示数-5的点的距离是2的点表示的数是( )
| A、-3 | B、-7 |
| C、±3 | D、-3或-7 |
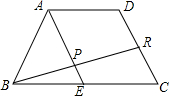 如图,B是平行四边形AECD边CE延长线上一点,且EB=EC,R为CD的中点,BR交AE于点P,则EP:AP=( )
如图,B是平行四边形AECD边CE延长线上一点,且EB=EC,R为CD的中点,BR交AE于点P,则EP:AP=( )A、
| ||
B、
| ||
C、
| ||
D、
|
若分式方程
-
=1产生增根,m的值是( )
| m |
| x+1 |
| 2 |
| x+1 |
| A、1 | B、2 | C、-1 | D、-2 |
 如图,在⊙O中,弦BC,BD关于直径AB所在直线对称.E为半径OC上一点,OC=3OE,连接AE并延长交⊙O于点F,连接DF交BC于点M.
如图,在⊙O中,弦BC,BD关于直径AB所在直线对称.E为半径OC上一点,OC=3OE,连接AE并延长交⊙O于点F,连接DF交BC于点M. 将图中的正方形纸片沿虚线剪开,可得到4个全等的直角三角形和一个小的正方形,你会用所得的5个张纸片分别拼出一个轴对称图形和一个中心对称图形吗?请画出你的作品.
将图中的正方形纸片沿虚线剪开,可得到4个全等的直角三角形和一个小的正方形,你会用所得的5个张纸片分别拼出一个轴对称图形和一个中心对称图形吗?请画出你的作品.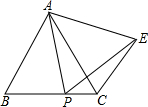 如图,△ABC是等边三角形,P为BC上一动点(不与B、C重合),以AP为边作等边△APE,连接CE.
如图,△ABC是等边三角形,P为BC上一动点(不与B、C重合),以AP为边作等边△APE,连接CE. 如图,AB是⊙O的直径,BE是弦,C是劣弧BE的中点,过C作CD⊥AB于D,CD交BE于点F,过C作CG∥BE交AB延长线于点G.
如图,AB是⊙O的直径,BE是弦,C是劣弧BE的中点,过C作CD⊥AB于D,CD交BE于点F,过C作CG∥BE交AB延长线于点G.