题目内容
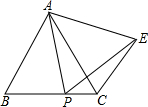 如图,△ABC是等边三角形,P为BC上一动点(不与B、C重合),以AP为边作等边△APE,连接CE.
如图,△ABC是等边三角形,P为BC上一动点(不与B、C重合),以AP为边作等边△APE,连接CE.(1)求证:AB∥CE;
(2)是否存在点P,使得AE⊥CE?若存在,指出点P的位置并证明你的结论;若不存,请说明理由.
考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:(1)根据等边三角形的性质得出角相等、边相等,证出△ABP≌△ACE(SAS),得出对应角相等,证出∠BAC=∠ACF,从而证出结论.
(2)由△ABP≌△ACE得出∠APB=∠AEC=90°,再由等边三角形的性质得出P为BC的中点.
(2)由△ABP≌△ACE得出∠APB=∠AEC=90°,再由等边三角形的性质得出P为BC的中点.
解答:证明:(1)∵△ABC、△APE是等边三角形,
∴∠BAC=∠PAE=∠B=60°,AB=AC,AF=AE,
∴∠BAP=∠CAE,
在△ABF和△ACE中,
∴△ABP≌△ACE(SAS),
∴∠B=∠ACP=60°,
∴∠BAC=∠ACF,
∴AB∥CE;
(2)存在点P使得AE⊥CE.此时P为BC的中点;理由如下:
∵AE⊥CE,
∴∠AEC=90°,
由(1)得:△ABP≌△ACE,
∴∠APB=∠AEC=90°,
∴AP⊥BC,
∵AB=AC,
∴P为BC的中点.
∴存在点P,使得AE⊥CE.
∴∠BAC=∠PAE=∠B=60°,AB=AC,AF=AE,
∴∠BAP=∠CAE,
在△ABF和△ACE中,
|
∴△ABP≌△ACE(SAS),
∴∠B=∠ACP=60°,
∴∠BAC=∠ACF,
∴AB∥CE;
(2)存在点P使得AE⊥CE.此时P为BC的中点;理由如下:
∵AE⊥CE,
∴∠AEC=90°,
由(1)得:△ABP≌△ACE,
∴∠APB=∠AEC=90°,
∴AP⊥BC,
∵AB=AC,
∴P为BC的中点.
∴存在点P,使得AE⊥CE.
点评:本题考查了等边三角形的性质以及全等三角形的判定与性质;由等边三角形证明三角形全等是关键.

练习册系列答案
相关题目
 把一张对边平行的纸条(AC∥BD)折成如图所示的那样,EF是折痕,若折痕EF与一边的夹角∠EFB=32°,你能求出∠AEG和∠EGB的度数吗?
把一张对边平行的纸条(AC∥BD)折成如图所示的那样,EF是折痕,若折痕EF与一边的夹角∠EFB=32°,你能求出∠AEG和∠EGB的度数吗?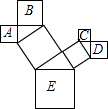 如图,图中所有的三角形都是直角三角形,四边形都是正方形.已知正方形A,B,C,D的边长分别是12,16,9,12,求最大正方形E的面积.
如图,图中所有的三角形都是直角三角形,四边形都是正方形.已知正方形A,B,C,D的边长分别是12,16,9,12,求最大正方形E的面积.
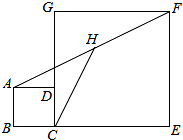 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是
如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是 如图,在梯形ABCD中,AD∥BC,∠DCB=90°,点E是边AB的中点,联结DE,延长DE交CB的延长线于点F,∠CBA=2∠F,且AC=BC.
如图,在梯形ABCD中,AD∥BC,∠DCB=90°,点E是边AB的中点,联结DE,延长DE交CB的延长线于点F,∠CBA=2∠F,且AC=BC.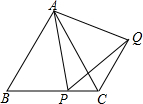 如图,已知△ABC为等边三角形,P为BC上一点,△APQ为等边三角形.
如图,已知△ABC为等边三角形,P为BC上一点,△APQ为等边三角形.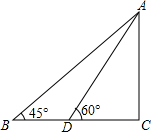 如图,在广场上用氢气球悬挂着“人文黔东南,和谐黔东南,美丽黔东南,建设黔东南”的大型宣传条幅AC.小明站在B处看条幅顶端A的仰角为45°,再往条幅方向前往20米到D处,在D处看条幅顶端A的仰角为60°,求条幅AC的高度(小明的身高不计,条幅垂直于地面)(结果精确到0.1米,参考数据
如图,在广场上用氢气球悬挂着“人文黔东南,和谐黔东南,美丽黔东南,建设黔东南”的大型宣传条幅AC.小明站在B处看条幅顶端A的仰角为45°,再往条幅方向前往20米到D处,在D处看条幅顶端A的仰角为60°,求条幅AC的高度(小明的身高不计,条幅垂直于地面)(结果精确到0.1米,参考数据