题目内容
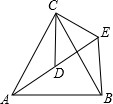 如图,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.
如图,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.(1)试探究线段AD、BE之间的数量关系是
(2)求出∠AEB的度数.
考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:(1)先证出∠ACD=∠BCE,那么△ACD≌△BCE,根据全等三角形证出AD=BE;
(2)∠ADC=∠BEC,求出∠ADC=120°,得出∠BEC=120°,从而证出∠AEB=60°.
(2)∠ADC=∠BEC,求出∠ADC=120°,得出∠BEC=120°,从而证出∠AEB=60°.
解答:
解:(1)AD=BE,理由如下:
∵△ACB和△DCE均为等边三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=60°,
∴∠ACD=60°-∠CDB=∠BCE.
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS).
∴AD=BE.
(2)∵△ACD≌△BCE,
∴∠ADC=∠BEC.
∵△DCE为等边三角形,
∴∠CDE=∠CED=60°.
∵点A,D,E在同一直线上,
∴∠ADC=120°,
∴∠BEC=120°.
∴∠AEB=∠BEC-∠CED=60°.
∵△ACB和△DCE均为等边三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=60°,
∴∠ACD=60°-∠CDB=∠BCE.
在△ACD和△BCE中,
|
∴△ACD≌△BCE(SAS).
∴AD=BE.
(2)∵△ACD≌△BCE,
∴∠ADC=∠BEC.
∵△DCE为等边三角形,
∴∠CDE=∠CED=60°.
∵点A,D,E在同一直线上,
∴∠ADC=120°,
∴∠BEC=120°.
∴∠AEB=∠BEC-∠CED=60°.
点评:此题考查了全等三角形的判定与性质和等边三角形的性质;证明三角形全等是解决问题的关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
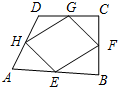 如图,已知四边形EFGH是四边形ABCD的中点四边形,若四边形EFGH是菱形,则原四边形ABCD可能为( )
如图,已知四边形EFGH是四边形ABCD的中点四边形,若四边形EFGH是菱形,则原四边形ABCD可能为( )| A、直角梯形 |
| B、平行四边形 |
| C、等腰梯形 |
| D、对角线互相垂直的四边形 |
一直三角形的两边长分别为3和4,则第三边长为( )
| A、5 | ||
B、5或
| ||
C、
| ||
| D、以上都不对 |
 如图,△ABC中,∠A=90°,试说明AB+AC>BC.
如图,△ABC中,∠A=90°,试说明AB+AC>BC. 如图,有下列判断:①∠A与∠1是同位角;②∠A与∠B是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角. 其中正确的是
如图,有下列判断:①∠A与∠1是同位角;②∠A与∠B是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角. 其中正确的是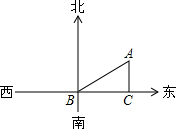 一艘船向东航行,上午8时到达B处,看到有一灯塔在它的北偏东59°,距离为72海里的A处,上午10时到达C处,看到灯塔在它的正北方向,求这艘船航行的速度.(精确到1海里/时)
一艘船向东航行,上午8时到达B处,看到有一灯塔在它的北偏东59°,距离为72海里的A处,上午10时到达C处,看到灯塔在它的正北方向,求这艘船航行的速度.(精确到1海里/时)