题目内容
4．在下列条件中，能够判定一个四边形是平行四边形的是（ ）| A． | 一组对边平行，另一组对边相等 | |
| B． | 一组对边相等，一组对角相等 | |
| C． | 一组对边平行，一条对角线平分另一条对角线 | |
| D． | 一组对边相等，一条对角线平分另一条对角线 |
分析 根据平行四边形的判定方法以及全等三角形的判定方法一一判断即可．
解答 解：A、错误．这个四边形有可能是等腰梯形．
B、错误．不满足三角形全等的条件，无法证明相等的一组对边平行．
C、正确．可以利用三角形全等证明平行的一组对边相等．故是平行四边形．
D、错误．不满足三角形全等的条件，无法证明相等的一组对边平行．
故选C．
点评 本题考查平行四边形的判定、全等三角形的判定和性质等知识，解题的关键是记住全等三角形的判定方法以及平行四边形的判定方法，属于中考常考题型．
练习册系列答案
全能测控期末小状元系列答案
相关题目
14．如果一组数据6，x，2，4的方差是5，那么数据x是（ ）
| A． | 10 | B． | 8 | C． | 4 | D． | 0或8 |
15．青山村种的水稻2010年平均每公顷产7200kg，2012年平均每公顷产8450kg，求水稻每公顷产量的年平均增长率，设水稻每公顷产量的年平均增长率为x，则所列方程正确的为（ ）
| A． | 7200（1+x）=8450 | B． | 7200（1+x）2=8450 | C． | 7200+x2=8450 | D． | 8450（1-x）2=7200 |
19．
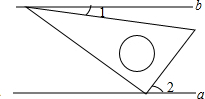如图，将一块含有60°角的直角三角板的两个顶点放在两条平行的直线a，b上，如果∠2=50°，那么∠1的度数为（ ）
如图，将一块含有60°角的直角三角板的两个顶点放在两条平行的直线a，b上，如果∠2=50°，那么∠1的度数为（ ）| A． | 10° | B． | 20° | C． | 30° | D． | 40° |
4．已知三点A（0，0），B（-4，0），C（-4，4），则△ABC是（ ）
| A． | 等边三角形 | B． | 等腰直角三角形 | C． | 钝角三角形 | D． | 无法判断形状 |
1．在⊙O上有顺次三点A，B，C，且$\widehat{AB}$=$\widehat{BC}$=$\widehat{CA}$，则△ABC的形状是（ ）
| A． | 等腰三角形 | B． | 直角三角形 | C． | 等边三角形 | D． | 等腰直角三角形 |
如图，四边形ABCD中，AB≠CD，E、F、G、H分别是AB、BD、CD、AC的中点．