题目内容
20.已知点P(2m+4,m-1),试分别根据下列条件,求出点P的坐标.(1)点P在y轴上;
(2)点P的纵坐标比横坐标大3;
(3)点P到x轴的距离为2,且在第四象限.
分析 (1)根据y轴上点的横坐标为0列方程求出m的值,再求解即可;
(2)根据纵坐标比横坐标大3列方程求解m的值,再求解即可;
(3)根据点P到x轴的距离列出绝对值方程求解m的值,再根据第四象限内点的横坐标是正数,纵坐标是负数求解.
解答 解:(1)∵点P(2m+4,m-1)在y轴上,
∴2m+4=0,
解得m=-2,
所以,m-1=-2-1=-3,
所以,点P的坐标为(0,-3);
(2)∵点P的纵坐标比横坐标大3,
∴(m-1)-(2m+4)=3,
解得m=-8,
m-1=-8-1=-9,
2m+4=2×(-8)+4=-12,
所以,点P的坐标为(-12,-9);
(3)∵点P到x轴的距离为2,
∴|m-1|=2,
解得m=-1或m=3,
当m=-1时,2m+4=2×(-1)+4=2,
m-1=-1-1=-2,
此时,点P(2,-2),
当m=3时,2m+4=2×3+4=10,
m-1=3-1=2,
此时,点P(10,2),
∵点P在第四象限,
∴点P的坐标为(2,-2).
点评 本题考查了点的坐标,熟练掌握坐标轴上点的坐标特征是解题的关键,(3)要注意点在第四象限.

练习册系列答案
 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
9.如果一个多边形的内角和等于它的外角和的2倍,则这个多边形是( )
| A. | 三角形 | B. | 四边形 | C. | 五边形 | D. | 六边形 |
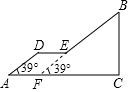 如图,人行天桥的引桥由楼梯和一段水平平台构成,楼梯AD与地面成39°,DE∥AC,楼梯EB与水平地面成39°角,已知BC=6m,AC=11m.
如图,人行天桥的引桥由楼梯和一段水平平台构成,楼梯AD与地面成39°,DE∥AC,楼梯EB与水平地面成39°角,已知BC=6m,AC=11m.

 已知△ABC的三边长分别为AB=2$\sqrt{5}$,AC=2,BC=4$\sqrt{\frac{1}{2}}$.
已知△ABC的三边长分别为AB=2$\sqrt{5}$,AC=2,BC=4$\sqrt{\frac{1}{2}}$.