题目内容
5.因市场竞争激烈,国商进行促销活动,决定对学习用品进行打八折出售,打折前,买2本笔记本和1支圆珠笔需要18元,买1本笔记本和2支圆珠笔需要12元.(1)求打折前1本笔记本,1支圆珠笔各需要多少元.
(2)在促销活动时间内,购买50本笔记本和40支圆珠笔共需要多少元?
分析 (1)设打折前1本笔记本需要x元,1支圆珠笔需要y元,根据打折前,买2本笔记本和1支圆珠笔需要18元,买1本笔记本和2支圆珠笔需要12元,列出方程组求解;
(2)根据(1)求出的单价直接求出打八折之后所需要的钱数即可.
解答 解:(1)设打折前1本笔记本需要x元,1支圆珠笔需要y元,
由题意得:$\left\{\begin{array}{l}{2x+y=18}\\{x+2y=12}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=8}\\{y=2}\end{array}\right.$,
答:打折前1本笔记本需要8元,1支圆珠笔需要2元;
(2)所需的钱数为:0.8×(50x+40y)=0.8×480=384(元).
答:购买50本笔记本和40支圆珠笔共需要384元.
点评 本题考查了二元一次方程组的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组求解.

练习册系列答案
相关题目
20.若x2-x-m=(x+n)(x+7),则m-n=( )
| A. | -64 | B. | -48 | C. | 48 | D. | 64 |
17.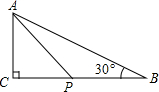 如图,△ABC中,∠C=90°,AC=2.5,∠B=30°,点P是BC边上的动点,则AP长不可能是( )
如图,△ABC中,∠C=90°,AC=2.5,∠B=30°,点P是BC边上的动点,则AP长不可能是( )
 如图,△ABC中,∠C=90°,AC=2.5,∠B=30°,点P是BC边上的动点,则AP长不可能是( )
如图,△ABC中,∠C=90°,AC=2.5,∠B=30°,点P是BC边上的动点,则AP长不可能是( )| A. | 3 | B. | 3.5 | C. | 4.8 | D. | 5.2 |
14.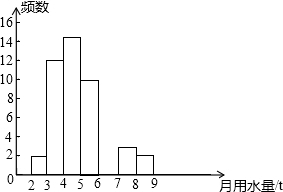 小亮同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了若干户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图)
小亮同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了若干户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图)
(1)频数分布表中a=15,b=30%.(填百分比),c=6;补全频数分布直方图.
(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有279户;
(3)从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,请用列表法或画树状图求抽取出的2个家庭来自不同范围的概率.
 小亮同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了若干户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图)
小亮同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了若干户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图)| 月均用水量(单位:t) | 频数 | 百分比 |
| 2≤x<3 | 2 | 4% |
| 3≤x<4 | 12 | 24% |
| 4≤x<5 | a | b |
| 5≤x<6 | 10 | 20% |
| 6≤x<7 | c | 12% |
| 7≤x<8 | 3 | 6% |
| 8≤x<9 | 2 | 4% |
(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有279户;
(3)从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,请用列表法或画树状图求抽取出的2个家庭来自不同范围的概率.
15. 如图,直角三角板的直角顶点落在直尺边上,若∠1=56°,则∠2的度数为( )
如图,直角三角板的直角顶点落在直尺边上,若∠1=56°,则∠2的度数为( )
 如图,直角三角板的直角顶点落在直尺边上,若∠1=56°,则∠2的度数为( )
如图,直角三角板的直角顶点落在直尺边上,若∠1=56°,则∠2的度数为( )| A. | 34° | B. | 44° | C. | 56° | D. | 28° |
 如图,在圆内接四边形ABCD中,O为圆心,∠BOD=160°,则∠BCD的度数为100°.
如图,在圆内接四边形ABCD中,O为圆心,∠BOD=160°,则∠BCD的度数为100°.