题目内容
利用二次函数图象求一元二次方程5x2+4x-2=0的近似根.
考点:图象法求一元二次方程的近似根
专题:
分析:根据函数与方程的关系,可得函数图象与x轴的交点的横坐标就是相应的方程的解.
解答: 解:方程5x2+4x-2=0根是函数y=5x2+4x-2与x轴交点的横坐标.
解:方程5x2+4x-2=0根是函数y=5x2+4x-2与x轴交点的横坐标.
作出二次函数y=5x2+4x-2的图象,如图所示,
由图象可知方程有两个根,一个在-2和-1之间,另一个在0和1之间.
先求-2和-1之间的根,
当x=-1.1时,y=-0.35;当x=-1.2时,y=0.4;
因此,x=-1.15是方程的一个近似根,
同理,x=0.35是方程的另一个近似根.
故一元二次方程5x2+4x-2=0的近似根为x=-1.15或0.35.
 解:方程5x2+4x-2=0根是函数y=5x2+4x-2与x轴交点的横坐标.
解:方程5x2+4x-2=0根是函数y=5x2+4x-2与x轴交点的横坐标.作出二次函数y=5x2+4x-2的图象,如图所示,
由图象可知方程有两个根,一个在-2和-1之间,另一个在0和1之间.
先求-2和-1之间的根,
当x=-1.1时,y=-0.35;当x=-1.2时,y=0.4;
因此,x=-1.15是方程的一个近似根,
同理,x=0.35是方程的另一个近似根.
故一元二次方程5x2+4x-2=0的近似根为x=-1.15或0.35.
点评:本题考查了图象法求一元二次方程的近似根,二次函数图象与x轴交点的横坐标是相应的一元二次方程的解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在菱形ABCD中,∠B=60°,点E,F分别从点B,D同时以同样的速度沿边BC,DC向点C运动.给出以下四个结论:①AE=AF;②∠CEF=∠CFE;③当点E,F分别为边BC,DC的中点时,△AEF是等边三角形;④当点E,F分别为边BC,DC的中点时,△AEF的面积最大.正确的是( )
如图,在菱形ABCD中,∠B=60°,点E,F分别从点B,D同时以同样的速度沿边BC,DC向点C运动.给出以下四个结论:①AE=AF;②∠CEF=∠CFE;③当点E,F分别为边BC,DC的中点时,△AEF是等边三角形;④当点E,F分别为边BC,DC的中点时,△AEF的面积最大.正确的是( )| A、①② | B、②③ |
| C、①②③ | D、.①②③④ |
 如图,在Rt△ABC中,∠C=90°,∠BAC=30°,点D是BC边上的点,CD=
如图,在Rt△ABC中,∠C=90°,∠BAC=30°,点D是BC边上的点,CD=| 3 |
A、2
| ||
B、
| ||
C、
| ||
| D、4 |
甲乙两人同时同地同向出发沿400米环形跑道跑步,甲的速度比乙快,当甲第二次追上乙时,甲比乙跑的路程( )
| A、一样多 | B、多800m |
| C、多400m | D、少400m |
 如图,已知∠1=∠2,若添一个条件就能使△ADE∽△ABC成立,则条件不能是( )
如图,已知∠1=∠2,若添一个条件就能使△ADE∽△ABC成立,则条件不能是( )| A、AD:AB=DE:BC |
| B、∠AED=∠C |
| C、∠D=∠B |
| D、AD:AB=AE:AC |
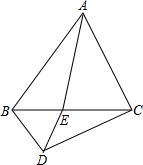 如图,△ABC是等边三角形,E为BC边上一点,将三角形ABE绕点B按顺时针方向旋转后,能与△CBD重合.若BE=3cm,则DE=
如图,△ABC是等边三角形,E为BC边上一点,将三角形ABE绕点B按顺时针方向旋转后,能与△CBD重合.若BE=3cm,则DE= 如图,在直角形坐标系中有两点A(6,0)、B(0,8),点C为AB的中点,点D在x轴上,当点D的坐标为
如图,在直角形坐标系中有两点A(6,0)、B(0,8),点C为AB的中点,点D在x轴上,当点D的坐标为