题目内容
 如图,在Rt△ABC中,∠C=90°,∠BAC=30°,点D是BC边上的点,CD=
如图,在Rt△ABC中,∠C=90°,∠BAC=30°,点D是BC边上的点,CD=| 3 |
A、2
| ||
B、
| ||
C、
| ||
| D、4 |
考点:翻折变换(折叠问题)
专题:
分析:如图,首先找出使△PEB的周长最小的点P的位置,然后求出BD、BE的长度,即可解决问题.
解答: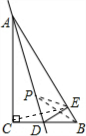 解:如图,连接CE;
解:如图,连接CE;
由题意知:C、E两点关于直线AD对称,DE=CD;
∴当点P在直线AD上运动到D点时,△PEB的周长最小,设为λ,
则λ=DE+BD+BE=CD+BD+BE;
∵在Rt△ABC中,∠C=90°,∠BAC=30°,
∴AB=2BC,AC=
BC,AB:AC=2:
;
∵AD平分∠BAC,
∴
=
,而CD=
,
∴BD=2;在直角△BDE中,
∵∠BED=90°-30°=60°,
∴cos60°=
,
∴BE=
BD=1,
∴λ=
+2+1=3+
,
故该题答案为C.
 解:如图,连接CE;
解:如图,连接CE;由题意知:C、E两点关于直线AD对称,DE=CD;
∴当点P在直线AD上运动到D点时,△PEB的周长最小,设为λ,
则λ=DE+BD+BE=CD+BD+BE;
∵在Rt△ABC中,∠C=90°,∠BAC=30°,
∴AB=2BC,AC=
| 3 |
| 3 |
∵AD平分∠BAC,
∴
| BD |
| CD |
| AB |
| AC |
| 3 |
∴BD=2;在直角△BDE中,
∵∠BED=90°-30°=60°,
∴cos60°=
| BE |
| BD |
∴BE=
| 1 |
| 2 |
∴λ=
| 3 |
| 3 |
故该题答案为C.
点评:该题主要考查了翻折变换的性质及其应用问题;解题的关键是根据翻折变换的性质找出图形中隐含的等量关系,大胆猜测,合情推理,科学论证.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在△ABC中,∠BAC=90°,AB=AC,若MN是经过点A的直线,BD⊥MN于D,CE⊥MN于E,求证:DE=BD+CE.
如图,在△ABC中,∠BAC=90°,AB=AC,若MN是经过点A的直线,BD⊥MN于D,CE⊥MN于E,求证:DE=BD+CE.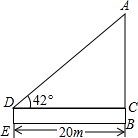 如图,升国旗时,某同学站在离国旗20m处行注目礼,当国旗升至顶端时,该同学视线的仰角为42°,已知双眼离地面1.60m,求旗杆AB的高度(精确到0.01m).
如图,升国旗时,某同学站在离国旗20m处行注目礼,当国旗升至顶端时,该同学视线的仰角为42°,已知双眼离地面1.60m,求旗杆AB的高度(精确到0.01m).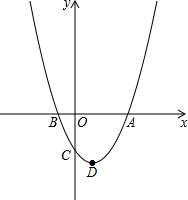 如图,已知抛物线y=ax2-2ax-b(a>0)与x轴的一个交点为B(-1,0),与y轴的负半轴交于点C,顶点为D.
如图,已知抛物线y=ax2-2ax-b(a>0)与x轴的一个交点为B(-1,0),与y轴的负半轴交于点C,顶点为D. 如图,△ABC中,BE平分∠ABC,CE平分∠ACB,DF经过点E,与AB,AC相交于点D,F,且DF∥BC.
如图,△ABC中,BE平分∠ABC,CE平分∠ACB,DF经过点E,与AB,AC相交于点D,F,且DF∥BC.