题目内容
10.已知菱形的边长为6,有一个内角是45°,则该菱形的面积是18$\sqrt{2}$.分析 作DE⊥AB于E,在Rt△ADE中,运用三角函数求出DE,即可求出菱形的面积=AB•DE.
解答 解:如图所示:作DE⊥AB于E, ∵四边形ABCD是菱形,
∵四边形ABCD是菱形,
∴AB=AD=6,
∵∠A=45°,
∴△ADE是等腰直角三角形,
∴AE=AD×sin45°=6×$\frac{\sqrt{2}}{2}$=3$\sqrt{2}$,
∴菱形ABCD的面积=AB•DE=6×3$\sqrt{2}$=18$\sqrt{2}$;
故答案为:18$\sqrt{2}$.
点评 本题考查了菱形的性质、三角函数以及菱形面积的计算方法;熟练掌握菱形的性质,运用三角函数求出高是解决问题的关键.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
5.已知∠1=55°,∠2与∠1互为余角,∠3与∠2互为邻补角,则∠3的度数为( )
| A. | 35° | B. | 145° | C. | 125° | D. | 55° |
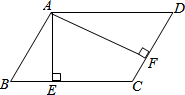 已知?ABCD的周长为36cm,过点A作AE⊥BC,AF⊥CD,若AE=2cm,AF=4cm,求平行四边形各边的长.
已知?ABCD的周长为36cm,过点A作AE⊥BC,AF⊥CD,若AE=2cm,AF=4cm,求平行四边形各边的长. 如图,两条平行线AB、CD被直线BC所截,一组同旁内角的平分线相交于点E,则∠BEC的度数是90°.
如图,两条平行线AB、CD被直线BC所截,一组同旁内角的平分线相交于点E,则∠BEC的度数是90°. 如图,△ABC是等边三角形,若点A绕点C顺时针旋转30°至点A′,联结A′B,则∠ABA′度数是15°.
如图,△ABC是等边三角形,若点A绕点C顺时针旋转30°至点A′,联结A′B,则∠ABA′度数是15°. 如图,AB是⊙O的直径,C,D两点在⊙O上,∠BCD=25°,则∠AOD的度数为130°.
如图,AB是⊙O的直径,C,D两点在⊙O上,∠BCD=25°,则∠AOD的度数为130°.