题目内容
16.联想三角形内心的概念,我们可引入如下概念.定义:到三角形的两边距离相等的点,叫做此三角形的准内心.
举例:如图1,若PD=PE,则点P为△ABC的准内心.
应用:如图2,BF为等边三角形的角平分线,准内心P在BF上,且PF=$\frac{1}{2}$BP,求证:点P是△ABC的内心.
探究:已知△ABC为直角三角形,∠C=90°,准内心P在AC上,若PC=$\frac{1}{2}$AP,求∠A的度数.
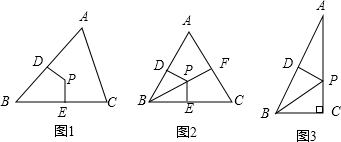
分析 应用:由△ABC是等边三角形,根据等边三角形的性质得到∠ABC=60°,由角平分线的性质∴∠PBE=30°,得到PE=$\frac{1}{2}$PB,因为BF是等边△ABC的角平分线,由三线合一得到BF⊥AC,PF=$\frac{1}{2}$BF,证得PE=PD=PF,得到结论P是△ABC的内心;
探究:根据题意得:PD=PC=$\frac{1}{2}$AP,由锐角三角函数得到结论.
解答 解:应用:∵△ABC是等边三角形,
∴∠ABC=60°,
∵BF为角平分线,
∴∠PBE=30°,
∴PE=$\frac{1}{2}$PB,
∵BF是等边△ABC的角平分线,
∴BF⊥AC,
∵PF=$\frac{1}{2}$BF,
∴PE=PD=PF,
∴P是△ABC的内心;
探究:根据题意得:
PD=PC=$\frac{1}{2}$AP,
∵$SinA=\frac{PD}{AP}=\frac{{\frac{1}{2}AP}}{AP}=\frac{1}{2}$,
∴∠A是锐角,
∴∠A=30°.
点评 此题考查了圆的综合,用到的知识点是角平分线的性质,特殊角的三角函数,等边三角形的性质,读懂题意,弄清楚准内心的定义是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.在平面直角坐标系中,将点A(-3,4)向右平移5个单位长度后,那么平移后对应的点A′的坐标是( )
| A. | (-3,-4) | B. | (2,4) | C. | (-3,9) | D. | (2,-1) |
5.已知∠1=55°,∠2与∠1互为余角,∠3与∠2互为邻补角,则∠3的度数为( )
| A. | 35° | B. | 145° | C. | 125° | D. | 55° |
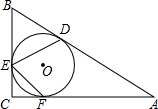 如图,在Rt△ABC中,∠C=90°,∠B=70°,△ABC的内切圆⊙O与边AB、BC、CA分别相切于点D、E、F,则∠DEF的度数为80°.
如图,在Rt△ABC中,∠C=90°,∠B=70°,△ABC的内切圆⊙O与边AB、BC、CA分别相切于点D、E、F,则∠DEF的度数为80°. 如图,两条平行线AB、CD被直线BC所截,一组同旁内角的平分线相交于点E,则∠BEC的度数是90°.
如图,两条平行线AB、CD被直线BC所截,一组同旁内角的平分线相交于点E,则∠BEC的度数是90°.