题目内容
19．先化简：（2-$\frac{4}{x+2}$）÷$\frac{x^2}{{{x^2}-4}}$，然后求当x=1时，这个代数式的值．分析 先根据分式混合运算的法则把原式进行化简，再把x=1代入进行计算即可．
解答 解：原式=$\frac{2x+4-4}{x+2}$•$\frac{（x+2）（x-2）}{{x}^{2}}$
=$\frac{2x}{x+2}$•$\frac{（x+2）（x-2）}{{x}^{2}}$
=$\frac{2（x-2）}{x}$，
当x=1时，原式=$\frac{2×（1-2）}{1}$=-2．
点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．
练习册系列答案
名校课堂系列答案
相关题目
9．
将矩形ABCD绕点B顺时针旋转90°后得到矩形A′BC′D′，若AB=12，AD=5，则△DBD′的面积为（ ）
将矩形ABCD绕点B顺时针旋转90°后得到矩形A′BC′D′，若AB=12，AD=5，则△DBD′的面积为（ ）| A． | 13 | B． | 26 | C． | 84.5 | D． | 169 |
7．下列事件中，属于不可能事件的是（ ）
| A． | 某班45位同学，其中有2位同学生日相同 | |
| B． | 在装只有10个红球的布袋中摸出一球，这球一定是红球 | |
| C． | 今天是星期五，明天就是星期日 | |
| D． | 同号两个实数的积一定是正数 |
11．掷一个质地均匀的正方体骰子，当骰子停止后，朝上一面的点数为3的概率是（ ）
| A． | 1 | B． | $\frac{1}{5}$ | C． | $\frac{1}{6}$ | D． | 0 |
8．
在平面直角坐标系中，矩形OABC如图所示．点A在x轴正半轴上，点C在y轴正半轴上，且OA=6，OC=4，D为OC中点，点E、F在线段OA上，点E在点F左侧，EF=3．当四边形BDEF的周长最小时，点E的坐标是（ ）
在平面直角坐标系中，矩形OABC如图所示．点A在x轴正半轴上，点C在y轴正半轴上，且OA=6，OC=4，D为OC中点，点E、F在线段OA上，点E在点F左侧，EF=3．当四边形BDEF的周长最小时，点E的坐标是（ ）| A． | （$\frac{1}{2}$，0） | B． | （1，0） | C． | （$\frac{3}{2}$，0） | D． | （2，0） |
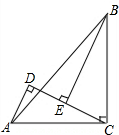已知：如图，在△ABC中，∠ACB=90°，AC=BC，BE⊥CE于点E，AD⊥CE于点D．求证：BE=CD．