题目内容
14.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次运动到点(2,0),第3次运动到点(3,-1),…,按照这样的运动规律,点P第2017次运动到点(2017,1).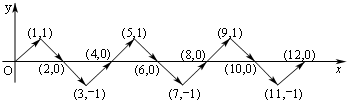
分析 令P点第n次运动到的点为Pn点(n为自然数).罗列出部分Pn点的坐标,根据点的坐标变化找出规律“P4n(4n,0),P4n+1(4n+1,1),P4n+2(4n+2,0),P4n+3(4n+3,-1)”,根据该规律即可得出结论.
解答 解:令P点第n次运动到的点为Pn点(n为自然数).
观察,发现规律:P0(0,0),P1(1,1),P2(2,0),P3(3,-1),P4(4,0),P5(5,1),…,
∴P4n(4n,0),P4n+1(4n+1,1),P4n+2(4n+2,0),P4n+3(4n+3,-1).
∵2017=4×504+1,
∴P第2017次运动到点(2017,1).
故答案为:(2017,1).
点评 本题考查了规律型中的点的坐标,解题的关键是发现规律“P4n(4n,0),P4n+1(4n+1,1),P4n+2(4n+2,0),P4n+3(4n+3,-1)”.本题属于基础题,难度不大,解决该题型题目时,根据点的变化罗列出部分点的坐标,根据坐标的变化找出变化规律是关键.

练习册系列答案
相关题目
5.若正比例函数y=kx与y=2x的图象关于x轴对称,则k的值等于( )
| A. | $\frac{1}{2}$ | B. | -2 | C. | -$\frac{1}{2}$ | D. | 2 |
3.二零一五年我国与“一带一路”国家贸易额达9955亿美元.数据9955用科学记数法表示为( )
| A. | 99.55×102 | B. | 9.955×103 | C. | 9.9×103 | D. | 10×103 |
 已知:当x>0时,反比例函数${y_1}=\frac{4}{x}$和y2=-$\frac{5}{x}$的图象在坐标系中的位置如图所示,直线y3=-x+b与两图象分别交于点A、B.
已知:当x>0时,反比例函数${y_1}=\frac{4}{x}$和y2=-$\frac{5}{x}$的图象在坐标系中的位置如图所示,直线y3=-x+b与两图象分别交于点A、B.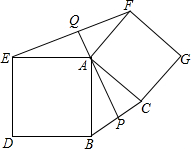 如图,两个正方形ABDE和ACGF,点P为BC中点,连接PA交EF于点Q,试探究AP与EF的数量和位置关系,并证明你的结论.
如图,两个正方形ABDE和ACGF,点P为BC中点,连接PA交EF于点Q,试探究AP与EF的数量和位置关系,并证明你的结论. 如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点A.与x轴、y轴分别交于点B、C,过点A作AD⊥x轴于点D,过点D作DE∥AB,交y轴于点E.己知四边形ADEC的面积为6.
如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点A.与x轴、y轴分别交于点B、C,过点A作AD⊥x轴于点D,过点D作DE∥AB,交y轴于点E.己知四边形ADEC的面积为6.