题目内容
17.计算:$\frac{x+2}{x+1}$-$\frac{x+3}{x+2}$-$\frac{x+4}{x+3}$+$\frac{x+5}{x+4}$.分析 原式分子变形后,逆用同分母分数的加法法则计算,通分并利用同分母分式的减法法则计算即可得到结果.
解答 解:原式=$\frac{x+1+1}{x+1}$-$\frac{x+2+1}{x+2}$-$\frac{x+3+1}{x+3}$+$\frac{x+4+1}{x+4}$
=1+$\frac{1}{x+1}$-1-$\frac{1}{x+2}$-1-$\frac{1}{x+3}$+1+$\frac{1}{x+4}$
=$\frac{1}{x+1}$+$\frac{1}{x+4}$-($\frac{1}{x+2}$+$\frac{1}{x+3}$)
=$\frac{2x+5}{(x+1)(x+4)}$-$\frac{2x+5}{(x+2)(x+3)}$
=(2x+5)•$\frac{{x}^{2}+5x+6-{x}^{2}-5x-4}{(x+1)(x+2)(x+3)(x+4)}$=$\frac{4x+10}{(x+1)(x+2)(x+3)(x+4)}$.
点评 此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
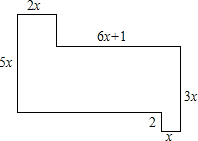 如图的面积为22x2+4x (以x来表示)
如图的面积为22x2+4x (以x来表示) 请只用无刻度的直尺作图:在图中的正方形网格边长均为1,在图(1)中作一个面积为12的菱形;在图(2)中作一个面积为13的正方形.
请只用无刻度的直尺作图:在图中的正方形网格边长均为1,在图(1)中作一个面积为12的菱形;在图(2)中作一个面积为13的正方形.