题目内容
14.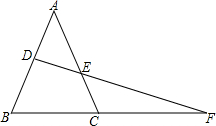 如图,在△ABC中,D为AB的中点,DF交AC于E,交BC的延长线于F,求证:AE•CF=BF•EC.
如图,在△ABC中,D为AB的中点,DF交AC于E,交BC的延长线于F,求证:AE•CF=BF•EC.
分析 过C作CG∥AB交DF于G,于是得到△GCF∽△DBF,△GCE∽△ADE,得到$\frac{CF}{BF}=\frac{CG}{BD}$,$\frac{EC}{AE}=\frac{CG}{AD}$,通过等量代换即可得到结论.
解答 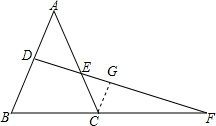 证明:过C作CG∥AB交DF于G,
证明:过C作CG∥AB交DF于G,
∴△GCF∽△DBF,△GCE∽△ADE,
∴$\frac{CF}{BF}=\frac{CG}{BD}$,$\frac{EC}{AE}=\frac{CG}{AD}$,
∵D为AB的中点,
∴AD=BD,
∴$\frac{CF}{BF}=\frac{CE}{AE}$,
∴AE•CF=BF•EC.
点评 本题主要考查了相似三角形的判定及其性质的应用问题,解题的关键是通过作辅助线构造相似三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,点P是矩形ABCD的边AD上一动点,矩形的两条 边长AB、BC分别为8和15,则点P到矩形的两条对角线AC和BD的距离之和为$\frac{120}{17}$.
如图,点P是矩形ABCD的边AD上一动点,矩形的两条 边长AB、BC分别为8和15,则点P到矩形的两条对角线AC和BD的距离之和为$\frac{120}{17}$.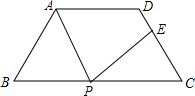 如图,在等腰梯形ABCD中,AD∥BC,AD=6cm,BC=14cm,∠B=60°,P为下底BC上一点(不与点B、C重合),连接AP,过点P作射线PE交线段DC于点E,使得∠APE=∠B,若DE:EC=5:3,则BP=2cm或12cm.
如图,在等腰梯形ABCD中,AD∥BC,AD=6cm,BC=14cm,∠B=60°,P为下底BC上一点(不与点B、C重合),连接AP,过点P作射线PE交线段DC于点E,使得∠APE=∠B,若DE:EC=5:3,则BP=2cm或12cm.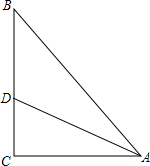 在Rt△ABC中,∠C=90°,tan∠CAD=$\frac{\sqrt{3}}{3}$,AB=14,AD=10,求BD的长.
在Rt△ABC中,∠C=90°,tan∠CAD=$\frac{\sqrt{3}}{3}$,AB=14,AD=10,求BD的长.