题目内容
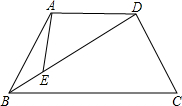 如图,在梯形ABCD中,AD∥BC,AB=CD=
如图,在梯形ABCD中,AD∥BC,AB=CD=| 10 |
考点:相似三角形的判定与性质,梯形
专题:计算题
分析:由AD与BC平行,根据两直线平行内错角相等可得出一对角相等,再由已知的两角相等,利用等量代换可得出∠BAE=∠BDA,再由∠ABE为公共角,利用两对对应角相等的两三角形相似得出三角形ABE与三角形BDA相似,根据相似得比例,将AB的值,及BD=x代入,用x表示出BE,用BD-BE表示出DE,再由梯形为等腰梯形,得到同一底上的两个角相等,由∠BAE=∠BDA,利用等式的性质得到∠EAD=∠CDB,再加上一对公共角相等,可得出三角形DAE与三角形BDC相似,由相似得比例,将BD=x,AD=y,BC的值,以及表示出的DE代入比例式,可得出y与x的关系式,并根据线段的长度大于0,梯形的上底小于下底,以及三角形的两边之和大于第三边,可得出自变量x的取值范围.
解答:解:∵AD∥BC,
∴∠ADB=DBC,
∵∠BAE=∠DBC,
∴∠BAE=∠BDA,…(1分)
∵∠ABE是公共角,
∴△BAE∽△BDA,…(2分)
∴
=
,又AB=
,BD=x,
∴
=
,
∴BE=
,…(5分)
∴DE=x-
,…(6分)
∵梯形ABCD中,AD∥BC,AB=DC,
∴∠BAD=∠CDA,又∠BAE=∠BDA,
∴∠BAD-∠BAE=∠CDA-∠BDA,即∠EAD=∠CDB,…(7分)
又∵∠ADE=∠DBC,
∴△DAE∽△BDC,…(8分)
∴
=
,又BD=x,AD=y,BC=5,DE=x-
,
∴
=
,…(10分)
∴y=
=
x2-2.…(11分)
定义域为5-
<x<5+
,且x≠
.…(13分)
∴∠ADB=DBC,
∵∠BAE=∠DBC,
∴∠BAE=∠BDA,…(1分)
∵∠ABE是公共角,
∴△BAE∽△BDA,…(2分)
∴
| BA |
| BD |
| BE |
| BA |
| 10 |
∴
| ||
| x |
| BE | ||
|
∴BE=
| 10 |
| x |
∴DE=x-
| 10 |
| x |
∵梯形ABCD中,AD∥BC,AB=DC,
∴∠BAD=∠CDA,又∠BAE=∠BDA,
∴∠BAD-∠BAE=∠CDA-∠BDA,即∠EAD=∠CDB,…(7分)
又∵∠ADE=∠DBC,
∴△DAE∽△BDC,…(8分)
∴
| DA |
| BD |
| DE |
| BC |
| 10 |
| x |
∴
| y |
| x |
x-
| ||
| 5 |
∴y=
| x2-10 |
| 5 |
| 1 |
| 5 |
定义域为5-
| 10 |
| 10 |
| 35 |
点评:此题考查了相似三角形的判定与性质,平行线的性质,等腰梯形的性质,以及三角形的边角关系,熟练掌握相似三角形的判定与性质是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,矩形ABCD中,AB=3,BC=6.分别以B、D为圆心,AB为半径画弧,两弧分别交对角线BD于点E、F,则图中阴影部分的面积为
如图,矩形ABCD中,AB=3,BC=6.分别以B、D为圆心,AB为半径画弧,两弧分别交对角线BD于点E、F,则图中阴影部分的面积为 到琴弦.(答案需为整数)
到琴弦.(答案需为整数)