题目内容
10.当x取何值时,下列分式的值为零?(1)$\frac{{x}^{2}-4}{x+2}$
(2)$\frac{{x}^{2}+2x-3}{|x|-1}$
(3)$\frac{{x}^{2}-1}{{x}^{2}-3x+2}$
(4)$\frac{5-|x|}{{x}^{2}+4x-5}$.
分析 (1)由分式值为0的条件可知;x2-4=0且x+2≠0,从而可解得x的值;
(2)由分式值为0的条件可知;x2+2x-3=0且|x|-1≠0,从而可解得x的值;
(3)由分式值为0的条件可知;x2-1=0且|x2-3x+2≠0,从而可解得x的值;
(4)由分式值为0的条件可知;5-|x=0且x2+4x-5≠0,从而可解得x的值.
解答 解:(1)∵分式值为0,
∴x2-4=0且x+2≠0,
解得x=2;
(2)∵分式值为0,
∴x2+2x-3=0且|x|-1≠0,
解得:x=-3;
(3)∵分式值为0,
∴x2-1=0且|x2-3x+2≠0,
解得:x=-1;
(4)∵分式值为0,
∴5-|x=0且x2+4x-5≠0,
∴x=±5,且(x+5)(x-1)≠0
∴x=5.
点评 本题主要考查的是分式值为零的条件和因式分解法解一元二次方程,掌握分式值为零的条件是解题的关键.

练习册系列答案
相关题目
 如图,⊙O直径AB=13cm,C为⊙O上的一点,已知CD⊥AB,垂足为D,并且CD=6cm,AD<DB,求AD的长.
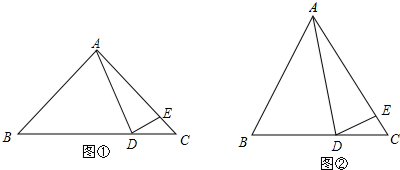
如图,⊙O直径AB=13cm,C为⊙O上的一点,已知CD⊥AB,垂足为D,并且CD=6cm,AD<DB,求AD的长. 如图,AB<BC,AD=DC,∠ABD=∠DBC,说明∠A+∠C=180°.
如图,AB<BC,AD=DC,∠ABD=∠DBC,说明∠A+∠C=180°.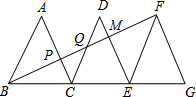 如图,已知△ABC,△DCE,△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=$\sqrt{3}$,BC=1,则BP=1.
如图,已知△ABC,△DCE,△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=$\sqrt{3}$,BC=1,则BP=1.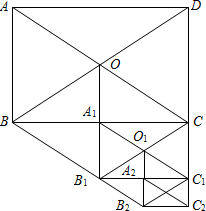 如图所示,在矩形ABCD中,AB=12,AC=20,两条对角线相交于点O.以OB、OC为邻边作第1个平行四边形OBB1C,对角线相交于点A1,再以A1B1、A1C为邻边作第2个平行四边形A1B1C1C,对角线相交于点O1;再以O1B1、O1C1为邻边作第3个平行四边形O1B1B2C1…依此类推.
如图所示,在矩形ABCD中,AB=12,AC=20,两条对角线相交于点O.以OB、OC为邻边作第1个平行四边形OBB1C,对角线相交于点A1,再以A1B1、A1C为邻边作第2个平行四边形A1B1C1C,对角线相交于点O1;再以O1B1、O1C1为邻边作第3个平行四边形O1B1B2C1…依此类推.