题目内容
20.已知a、b为有理数,且a+b、a-b、ab、$\frac{a}{b}$中恰有三个数相等,求(2a)-2015b的值.分析 解答此题先判断出a+b≠a-b,再进行分类,根据题意组合成ab=$\frac{a}{b}$=a+b或ab=$\frac{a}{b}$=a-b来解答
解答 解:∵b≠0,
∴a+b≠a-b,
因此只有a=0或b=±1,
若a=0,则必须b=0,矛盾,
若b=1,则ab,$\frac{a}{b}$,a+b,a-b中不可能有三个数相等,
当b=-1时,有ab=$\frac{a}{b}$=a+b或ab=$\frac{a}{b}$=a-b,
对应的a值分别为-$\frac{1}{2}$或$\frac{1}{2}$,
∴(2a)-2015b=(±1)2015=±1.
点评 此题考查代数式求值,蕴含了分类讨论和反证法等思想方法,有较强的逻辑性,需要仔细、认真.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
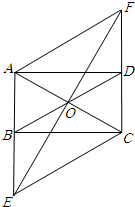 如图,矩形ABCD中,O是AC与BD的交点,过O点的直线EF与AB,CD的延长线分别交于E,F.
如图,矩形ABCD中,O是AC与BD的交点,过O点的直线EF与AB,CD的延长线分别交于E,F.