题目内容
5.计算:(1)$\sqrt{9}+\root{3}{-8}-\sqrt{1+\frac{9}{16}}$;
(2)|-2|+($\frac{1}{3}$)-1×(π-$\sqrt{2}$)0-$\sqrt{9}$+(-1)2.
分析 (1)首先化简各根式,再进行减法运算即可;
(2)本题涉及绝对值、负整数指数幂、零指数幂、二次根式化简、有理数的乘方5个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
解答 解:(1)$\sqrt{9}+\root{3}{-8}-\sqrt{1+\frac{9}{16}}$
=3-2-$\frac{5}{4}$
=-$\frac{1}{4}$;
(2)|-2|+($\frac{1}{3}$)-1×(π-$\sqrt{2}$)0-$\sqrt{9}$+(-1)2
=2+3×1-3+1
=3.
点评 本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握负整数指数幂、零指数幂、二次根式、绝对值等考点的运算.

练习册系列答案
相关题目
15.从2开始,连续的偶数相加,它们和的情况如下表:
(1)若n=9时,则S的值为90;
(2)根据表中的规律猜想:用n的代数式表示S的公式为:S=2+4+6+8+…+2n=n(n+1);
(3)根据上题的规律计算:102+104+106+108+…+1008的值.(要求写出过程)
| 加数的个数n | 连续偶数的和S |
| 1 | 2=1×2 |
| 2 | 2+4=6=2×3 |
| 3 | 2+4+6=12=3×4 |
| 4 | 2+4+6+8=20=4×5 |
| 5 | 2+4+6+8+10=30=5×6 |
(2)根据表中的规律猜想:用n的代数式表示S的公式为:S=2+4+6+8+…+2n=n(n+1);
(3)根据上题的规律计算:102+104+106+108+…+1008的值.(要求写出过程)
 如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数.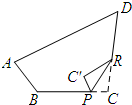 如图,将四边形纸片ABCD的右下角向内折出△PC′R,其中∠B=120°,∠D=40°,恰使C′P∥AB,RC′∥AD,则∠C=100°.
如图,将四边形纸片ABCD的右下角向内折出△PC′R,其中∠B=120°,∠D=40°,恰使C′P∥AB,RC′∥AD,则∠C=100°.