题目内容
 如图,AD是△ABC的中线,E是AD的中点,BE的延长线与AC交于F,则AF:AC等于( )
如图,AD是△ABC的中线,E是AD的中点,BE的延长线与AC交于F,则AF:AC等于( )| A、1:2 | B、1:3 |
| C、2:3 | D、2:5 |
考点:平行线分线段成比例
专题:
分析:先过D作BF的平行线,交AC边于G,得出DG∥BF,再根据D为BC中点可得出△CDG∽△CBF,即
=
=
,CG=
FC=FG;同理得出△AEF∽△ADG,AF=
AG=FG,从而得出AF=FG=GC,即可得出AF:AC的值.
| CG |
| CF |
| CD |
| CB |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:过D作BF的平行线,交AC边于G,如下图所示:
解:过D作BF的平行线,交AC边于G,如下图所示:
∵D为BC中点,DG∥BF,
∴∠CGD=∠CFB,
又∵∠C=∠C,
∴△CDG∽△CBF,
∴
=
=
,即:CG=
CF=FG,
又E为AD的中点,BE的延长线交AC于F,DG∥BF,
同理可得:△AEF∽△ADG,
∴
=
=
,即:AF=
AG=FG,
∴AF=FG=GC,
∴AF:AC=1:3,
故选:B.
 解:过D作BF的平行线,交AC边于G,如下图所示:
解:过D作BF的平行线,交AC边于G,如下图所示:∵D为BC中点,DG∥BF,
∴∠CGD=∠CFB,
又∵∠C=∠C,
∴△CDG∽△CBF,
∴
| CG |
| CF |
| CD |
| CB |
| 1 |
| 2 |
| 1 |
| 2 |
又E为AD的中点,BE的延长线交AC于F,DG∥BF,
同理可得:△AEF∽△ADG,
∴
| AE |
| AD |
| AF |
| AG |
| 1 |
| 2 |
| 1 |
| 2 |
∴AF=FG=GC,
∴AF:AC=1:3,
故选:B.
点评:此题考查了平行线分线段成比例,用到的知识点是相似三角形的判定与性质,关键在于找出条件判断两个三角形相似,再运用相似三角形的性质求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
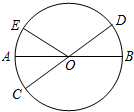 如图,AB,CD是⊙O的直径,
如图,AB,CD是⊙O的直径, |
| AE |
 |
| BD |
| A、32° | B、60° |
| C、68° | D、64° |
根据图中数字的规律,最后一个空格应填的数是( )

| A、738 | B、720 |
| C、550 | D、500 |
已知直角三角形ABC的一条直角边AB=4cm,另一条直角边BC=3cm,则以AB为轴旋转一周,所得到的圆锥的侧面积是( )
| A、30πcm2 |
| B、15πcm2 |
| C、12πcm2 |
| D、20πcm2 |
 小红和小兰房间窗户都是长宽分别为a厘米、4b厘米的窗户,窗户上的装饰布如图所示,它们分别由两个相同的半圆和两个相同的四分之一圆组成的.
小红和小兰房间窗户都是长宽分别为a厘米、4b厘米的窗户,窗户上的装饰布如图所示,它们分别由两个相同的半圆和两个相同的四分之一圆组成的.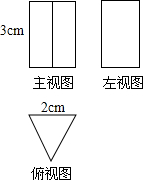 如图是一个几何体从三个方向看所得到的形状图.
如图是一个几何体从三个方向看所得到的形状图.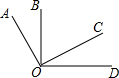 如图,OA⊥OC,OB⊥OD,①∠AOB=∠COD;②∠BOC+∠AOD=180°;③∠AOB+∠COD=90°;④图中小于平角的角有6个;其中正确的结论有几个( )
如图,OA⊥OC,OB⊥OD,①∠AOB=∠COD;②∠BOC+∠AOD=180°;③∠AOB+∠COD=90°;④图中小于平角的角有6个;其中正确的结论有几个( )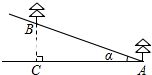 如图,在山坡上植树,已知山坡的倾斜角α是20°,小明种植的两棵树间的坡面距离AB是6米,要求相邻两棵树间的水平距离AC在5.3~5.5米范围内,问小明种植的这两棵树是否符合这个要求?
如图,在山坡上植树,已知山坡的倾斜角α是20°,小明种植的两棵树间的坡面距离AB是6米,要求相邻两棵树间的水平距离AC在5.3~5.5米范围内,问小明种植的这两棵树是否符合这个要求?