题目内容
18．
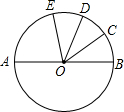如图，AB是⊙O的直径，$\widehat{BC}$=$\widehat{CD}$=$\widehat{DE}$，∠COD=35°，求∠AOE的度数．
分析 根据弧与圆心角的关系，即可求得∠BOC=∠COD=∠DOE=35°，得出∠BOE=105°，从而求得∠AOE=75°．．
解答 解：∵AB是⊙O的直径，$\widehat{BC}$=$\widehat{CD}$=$\widehat{DE}$，∠COD=35°，
∴∠BOC=∠COD=∠DOE=35°．
∴∠BOE=105°，
∴∠AOE=180°-105°=75°．
点评 此题考查了弧与圆心角的关系．此题比较简单，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
8．下列语句中，不是命题的是（ ）
| A． | 若两角之和为90°，则这两个角互余 | B． | 延长线段AO到点C，使OC=OA | ||
| C． | 平角是一条直线 | D． | 相等的角是对顶角 |
9．下列等式正确的是（ ）
| A． | （-x2）3=-x5 | B． | x3+x3=2x6 | C． | a3•a3=2a3 | D． | 26+26=27 |
13．在平面直角坐标系中，点P（2，-1）关于原点O的对称点在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
3．将二次函数y=x2+1的图象向右平移1个单位，则平移后的二次函数的解析式为（ ）
| A． | y=x2 | B． | y=（x-1）2 | C． | y=（x-1）2+1 | D． | y=（x+1）2+1 |
