题目内容
13.如图所示,点A、B在直线MN上,AB=11cm,⊙A、⊙B的半径均为1cm,⊙A以每秒2cm 的速度自左向右运动,与此同时,⊙B的半径也在不断增大,其半径r(cm)与时间t(秒)之间的关系式为r=1+t(t≥0),当⊙A出发后几秒两圆外切?在运动过程中,两圆会内切吗?如果会,求⊙A的运动时间,如果不会,说明理由.
分析 根据两圆相切时,两圆的半径与圆心距的关系,注意有4种情况.
解答  解:分四种情况考虑:
解:分四种情况考虑:
①当首次外切时,有2t+1+1+t=11,解得:t=3;
②当首次内切时,有2t+1+t-1=11,解得:t=$\frac{11}{3}$;
③当再次内切时,有2t-(1+t-1)=11,解得:t=11;
④当再次外切时,有2t-(1+t)-1=11,解得:t=13.
∴当点A出发后3、$\frac{11}{3}$、11、13秒两圆相切.
点评 本题考查了两圆相切时,两圆的半径与圆心距的关系,注意有4种情况.

练习册系列答案
相关题目
1.为了了解全校七年级439名学生的视力情况,骆老师从中抽查了45名学生的视力情况.针对这个问题,下面说法正确的是( )
| A. | 439名学生是总体 | B. | 每名学生是个体 | ||
| C. | 这个样本容量是45 | D. | 45名学生是所抽取的一个样本 |
8.沿河两地相距m千米,船在静水中的速度为b千米/时,水流的速度为c千米/时,则船往返一次所需的时间是( )
| A. | $\frac{2m}{b+c}$小时 | B. | ($\frac{m}{b+c}$+$\frac{m}{b-c}$)小时 | C. | $\frac{2m}{b-c}$小时 | D. | ($\frac{m}{b}$+$\frac{m}{c}$)小时 |
3.化简:
| (1)$\sqrt{72}$; | (2)$\sqrt{48}$; | (3)$\sqrt{\frac{2}{3}}$; |
| (4)-2$\sqrt{\frac{9}{2}}$; | (5)$\sqrt{{a}^{3}b}$(a≤0); | (6)$\sqrt{{a}^{4}+2{a}^{2}{b}^{2}+{b}^{4}}$. |
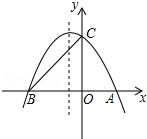 如图,抛物线与x轴交于A、B两点,与y轴交C点,点A的坐标为(2,0),点B的坐标为(-3,0),点C的坐标为(0,3),
如图,抛物线与x轴交于A、B两点,与y轴交C点,点A的坐标为(2,0),点B的坐标为(-3,0),点C的坐标为(0,3),