题目内容
6.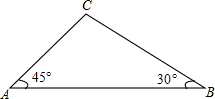 如图,天星山山脚下西端A处与东端B处相距800(1+$\sqrt{3}$)米,小军和小明同时分别从A处和B处向山顶C匀速行走.已知山的西端的坡角是45°,东端的坡角是30°,小军的行走速度为$\frac{\sqrt{2}}{2}$米/秒.若小明与小军同时到达山顶C处,则小明的行走速度是多少?
如图,天星山山脚下西端A处与东端B处相距800(1+$\sqrt{3}$)米,小军和小明同时分别从A处和B处向山顶C匀速行走.已知山的西端的坡角是45°,东端的坡角是30°,小军的行走速度为$\frac{\sqrt{2}}{2}$米/秒.若小明与小军同时到达山顶C处,则小明的行走速度是多少?
分析 过点C作CD⊥AB于点D,设AD=x米,小明的行走速度是a米/秒,根据直角三角形的性质用x表示出AC与BC的长,再根据小明与小军同时到达山顶C处即可得出结论.
解答  解:过点C作CD⊥AB于点D,设AD=x米,小明的行走速度是a米/秒,
解:过点C作CD⊥AB于点D,设AD=x米,小明的行走速度是a米/秒,
∵∠A=45°,CD⊥AB,
∴AD=CD=x米,
∴AC=$\sqrt{2}$x.
在Rt△BCD中,
∵∠B=30°,
∴BC=$\frac{CD}{sin30°}$=$\frac{x}{\frac{1}{2}}$=2x,
∵小军的行走速度为$\frac{\sqrt{2}}{2}$米/秒.若小明与小军同时到达山顶C处,
∴$\frac{\sqrt{2}x}{\frac{\sqrt{2}}{2}}$=$\frac{2x}{a}$,解得a=1米/秒.
答:小明的行走速度是1米/秒.
点评 本题考查的是解直角三角形的应用-坡度坡角问题,根据题意作出辅助线,利用锐角三角函数的定义求解是解答此题的关键.

练习册系列答案
相关题目
17.三张外观相同的卡片分别标有数字1、2、3,从中随机一次抽出两张,这两张卡片上的数字恰好都小于3的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{9}$ |
11.地球上的海洋面积为361 000 000平方千米,数字361 000 000用科学记数法表示为( )
| A. | 36.1×107 | B. | 0.361×109 | C. | 3.61×108 | D. | 3.61×107 |
16.2015年我县有880名初中毕业生参加升学考试为了了解这880名考生的数学成绩,从中抽取200名考生的数学成绩进行统计,在这个问题中样本是( )
| A. | 880名考生 | B. | 200名考生 | ||
| C. | 880名考生的数学成绩 | D. | 200名考生的数学成绩 |
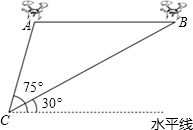 某兴趣小组借助无人飞机航拍校园.如图,无人飞机从A处水平飞行至B处需8秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)
某兴趣小组借助无人飞机航拍校园.如图,无人飞机从A处水平飞行至B处需8秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)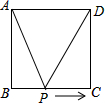 如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )
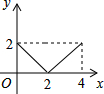
如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )


 如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.
如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.