题目内容
15. 如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.
如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.(1)求证:四边形AECF是菱形;
(2)若AB=$\sqrt{3}$,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
分析 (1)由过AC的中点O作EF⊥AC,根据线段垂直平分线的性质,可得AF=CF,AE=CE,OA=OC,然后由四边形ABCD是矩形,易证得△AOF≌△COE,则可得AF=CE,继而证得结论;
(2)由四边形ABCD是矩形,易求得CD的长,然后利用三角函数求得CF的长,继而求得答案.
解答 (1)证明:∵O是AC的中点,且EF⊥AC,
∴AF=CF,AE=CE,OA=OC,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠AFO=∠CEO,
在△AOF和△COE中,
$\left\{\begin{array}{l}{∠AFO=∠CEO}\\{∠AOF=∠COE}\\{OA=OC}\end{array}\right.$,
∴△AOF≌△COE(AAS),
∴AF=CE,
∴AF=CF=CE=AE,
∴四边形AECF是菱形;
(2)解:∵四边形ABCD是矩形,
∴CD=AB=$\sqrt{3}$,
在Rt△CDF中,cos∠DCF=$\frac{CD}{CF}$,∠DCF=30°,
∴CF=$\frac{CD}{cos30°}$=2,
∵四边形AECF是菱形,
∴CE=CF=2,
∴四边形AECF是的面积为:EC•AB=2$\sqrt{3}$.
点评 此题考查了矩形的性质、菱形的判定与性质以及三角函数等知识.注意证得△AOF≌△COE是关键.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
5. 在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:
在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:
5640 6430 6520 6798 7325
8430 8215 7453 7446 6754
7638 6834 7326 6830 8648
8753 9450 9865 7290 7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
步数分组统计表
请根据以上信息解答下列问题:
(1)填空:m=4,n=1;
(2)补全频数发布直方图;
(3)这20名“健步走运动”团队成员一天行走步数的中位数落在B组;
(4)若该团队共有120人,请估计其中一天行走步数不少于7500步的人数.
 在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:
在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:5640 6430 6520 6798 7325
8430 8215 7453 7446 6754
7638 6834 7326 6830 8648
8753 9450 9865 7290 7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
步数分组统计表
| 组别 | 步数分组 | 频数 |
| A | 5500≤x<6500 | 2 |
| B | 6500≤x<7500 | 10 |
| C | 7500≤x<8500 | m |
| D | 8500≤x<9500 | 3 |
| E | 9500≤x<10500 | n |
(1)填空:m=4,n=1;
(2)补全频数发布直方图;
(3)这20名“健步走运动”团队成员一天行走步数的中位数落在B组;
(4)若该团队共有120人,请估计其中一天行走步数不少于7500步的人数.
20.我市气象部门测得某周内七天的日温差数据如下:4,6,6,5,7,6,8(单位:℃),这组数据的平均数和众数分别是( )
| A. | 7,6 | B. | 6,5 | C. | 5,6 | D. | 6,6 |
7.下列图形都是由同样大小的基本图形按一定规律所组成的,其中第①个图形中一共有5个基本图形,第②个图形中一共有8个基本图形,第③个图形中一共有11个基本图形,第④个图形中一共有14个基本图形,…,按此规律排列,则第⑧个图形中基本图形的个数为( )
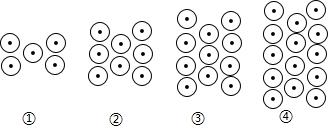

| A. | 23 | B. | 24 | C. | 26 | D. | 29 |
4.下列计算中,正确的是( )
| A. | (-ab)2=a2b2 | B. | a•a3=a3 | C. | a6÷a2=a3 | D. | 2a+3b=5ab |
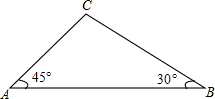 如图,天星山山脚下西端A处与东端B处相距800(1+$\sqrt{3}$)米,小军和小明同时分别从A处和B处向山顶C匀速行走.已知山的西端的坡角是45°,东端的坡角是30°,小军的行走速度为$\frac{\sqrt{2}}{2}$米/秒.若小明与小军同时到达山顶C处,则小明的行走速度是多少?
如图,天星山山脚下西端A处与东端B处相距800(1+$\sqrt{3}$)米,小军和小明同时分别从A处和B处向山顶C匀速行走.已知山的西端的坡角是45°,东端的坡角是30°,小军的行走速度为$\frac{\sqrt{2}}{2}$米/秒.若小明与小军同时到达山顶C处,则小明的行走速度是多少?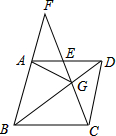 如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.
如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.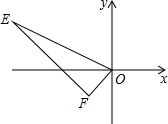 如图,点E(-4,2),F(-1,-1),以点O为位似中心,在点O的另一侧,按比例尺1:2,把△EFO缩小,则点E的对应点E′的坐标为(2,-1).
如图,点E(-4,2),F(-1,-1),以点O为位似中心,在点O的另一侧,按比例尺1:2,把△EFO缩小,则点E的对应点E′的坐标为(2,-1).