题目内容
2.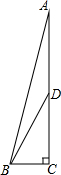 (1)计算:sin30°+3tan60°-cos245°.
(1)计算:sin30°+3tan60°-cos245°.(2)如图,在Rt△ABC中,∠C=90°,∠ABC=75°,D在AC上,DC=6,∠DBC=60°,求AD的长.
分析 (1)将特殊角的三角函数值代入求解;
(2)根据三角函数的定义和直角三角形的解法解答即可.
解答 解:(1)sin30°+3tan60°-cos245°
=$\frac{1}{2}+3\sqrt{3}-(\frac{\sqrt{2}}{2})^{2}$
=$\frac{1}{2}+3\sqrt{3}-\frac{1}{2}$
=$3\sqrt{3}$;
(2)Rt△DBC 中,sin∠DBC=$\frac{DC}{BD}$,
sin60°=$\frac{6}{BD}$,
$\frac{\sqrt{3}}{2}=\frac{6}{BD}$,
BD=4$\sqrt{3}$,
∠ABD=∠ABC-∠DBC=75°-60°=15°,
∠A+∠ABC=90°,
∠A=90°-∠ABC=90°-75°=15°,
∴∠ABD=∠A,
∴AD=BD=4$\sqrt{3}$.
点评 本题考查了特殊角的三角函数值,解答本题的关键是掌握几个特殊角的三角函数值.

练习册系列答案
相关题目
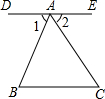
13. 如图,下列说法中错误的是( )
如图,下列说法中错误的是( )
 如图,下列说法中错误的是( )
如图,下列说法中错误的是( )| A. | ∠1、∠3是同位角 | B. | ∠1、∠2是同旁内角 | C. | ∠1、∠5是同位角 | D. | ∠5、∠6是内错角 |
10.下列命题中,正确的个数是( )
①若三条线段的比为1:1:$\sqrt{2}$,则它们组成一个等腰直角三角形;
②两条对角线相等的四边形是平行四边形;
③对角线互相平分四边形是平行四边形;
④两个邻角相等的四边形是平行四边形.
①若三条线段的比为1:1:$\sqrt{2}$,则它们组成一个等腰直角三角形;
②两条对角线相等的四边形是平行四边形;
③对角线互相平分四边形是平行四边形;
④两个邻角相等的四边形是平行四边形.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.某学习小组中有甲、乙、丙、丁四位同学,为解决尺规作图:“过直线AB外一点M,作一直线垂直于直线AB”,各自提供了如下四种方案,其中正确的是( )
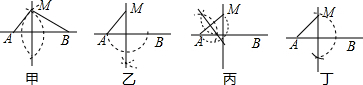
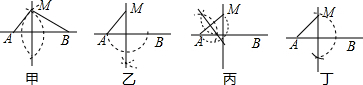
| A. | 甲、乙 | B. | 乙、丙 | C. | 丙、丁 | D. | 甲、乙、丙 |
 完成下列推理过程.
完成下列推理过程.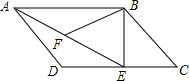 如图所示,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上一点,且∠BFE=∠C.
如图所示,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上一点,且∠BFE=∠C. 如图,AD,AC分别是⊙O的直径和弦,∠CAD=30°,B是AC上一点,BO⊥AD,垂足为O,CD=3cm,求BO的长及劣弧CD的长.
如图,AD,AC分别是⊙O的直径和弦,∠CAD=30°,B是AC上一点,BO⊥AD,垂足为O,CD=3cm,求BO的长及劣弧CD的长.