题目内容
9.先阅读下列解法,再解答后面的问题.已知$\frac{3x-4}{{x}^{2}-3x+2}$=$\frac{A}{x-1}$+$\frac{B}{x-2}$,求A、B的值.
解法一:将等号右边通分,再去分母,得:3x-4=A(x-2)+B(x-1),
即:3x-4=(A+B)x-(2A+B),
∴$\left\{\begin{array}{l}A+B=3\\-(2A+B)=-4\end{array}\right.$.
解得 $\left\{\begin{array}{l}A=1\\ B=2\end{array}\right.$.
解法二:在已知等式中取x=0,有-A+$\frac{B}{-2}$=-2,整理得
2A+B=4;
取x=3,有$\frac{A}{2}$+B=$\frac{5}{2}$,整理得
A+2B=5.
解 $\left\{\begin{array}{l}2A+B=4\\ A+2B=5\end{array}\right.$,
得:$\left\{\begin{array}{l}A=1\\ B=2\end{array}\right.$.
(1)已知$\frac{11x}{{-3{x^2}-14x+24}}=\frac{A}{x+6}+\frac{B}{4-3x}$,用上面的解法一或解法二求A、B的值.
(2)计算:
[$\frac{1}{{(x-1)({x+1})}}+\frac{1}{(x+1)(x+3)}+\frac{1}{(x+3)(x+5)}+…+\frac{1}{(x+9)(x+11)}$](x+11),并求x取何整数时,这个式子的值为正整数.
分析 (1)根据方法一可得11x=A(4-3x)+B(x+6),即11x=(-3A+B)x+(4A+6B),得出$\left\{\begin{array}{l}{-3A+B=11}\\{4A+6B=0}\end{array}\right.$,解之可得答案;
(2)裂项求解可得原式=$\frac{6}{x-1}$,由式子的值为正整数知x-1=1、2、3、6,从而得出答案.
解答 解:(1)等号右边通分、再去分母,得:11x=A(4-3x)+B(x+6),
即11x=(-3A+B)x+(4A+6B),
∴$\left\{\begin{array}{l}{-3A+B=11}\\{4A+6B=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{A=-3}\\{B=2}\end{array}\right.$;
(2)原式=$\frac{1}{2}$($\frac{1}{x-1}$-$\frac{1}{x+1}$+$\frac{1}{x+1}$-$\frac{1}{x+3}$+$\frac{1}{x+3}$-$\frac{1}{x+5}$+…+$\frac{1}{x+9}$-$\frac{1}{x+11}$)×(x+11)
=$\frac{1}{2}$×($\frac{1}{x-1}$-$\frac{1}{x+11}$)×(x+11)
=$\frac{1}{2}$×$\frac{12}{(x-1)(x+11)}$×(x+11)
=$\frac{6}{x-1}$,
∵式子的值为正整数,
∴x-1=1、2、3、6,
则x=2、3、4、7.
点评 本题主要考查分式的化简求值,熟练掌握分式的混合运算顺序和法则及裂项求解的方法是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
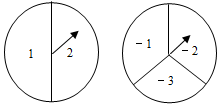 如图,有A、B两个转盘,A转盘被二等分,分别标有数字1和2.B转盘被三等分,分别标有数字-1,-2和-3.小强分别转动A盘、B盘各一次(若指针恰好指在分割线上,则重转一次,直到指针指向一个数字为止).记录A盘指针所对区域的数字为a,B盘指针所对区域的数字为b,这样就确定点Q的一个坐标为(a,b).
如图,有A、B两个转盘,A转盘被二等分,分别标有数字1和2.B转盘被三等分,分别标有数字-1,-2和-3.小强分别转动A盘、B盘各一次(若指针恰好指在分割线上,则重转一次,直到指针指向一个数字为止).记录A盘指针所对区域的数字为a,B盘指针所对区域的数字为b,这样就确定点Q的一个坐标为(a,b).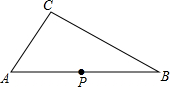 如图,点P是三角形ABC的边AB上一点,
如图,点P是三角形ABC的边AB上一点,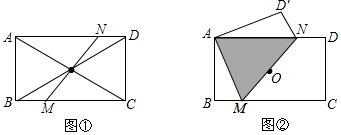
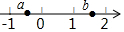 有理数a、b在数轴上的位置如图所示,则|a+1|-|b-2|的结果为a+b-1.
有理数a、b在数轴上的位置如图所示,则|a+1|-|b-2|的结果为a+b-1.