题目内容
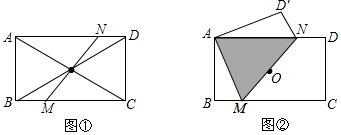
1.如图,在矩形ABCD中,AD>AB,O为对角线AC、BD的交点,过点O作一直线分别交BC、AD于点M、N.(1)试用中心对称的性质说明梯形ABMN的面积等于梯形CDNM的面积;
(2)若将矩形ABCD沿MN翻折后,点C恰好与点A重合,则MN满足什么条件(只要求写出满足的条件,不要求说明理由)?
(3)在(2)条件下若翻折后不重叠部分(△ABM的面积是重叠部分(阴影部分)面积的$\frac{1}{2}$(如图②),请探究BM与MC之间的数量关系.
分析 (1)根据矩形的对角线互相平分可得AO=CO,再根据两直线平行,内错角相等可得∠MCO=∠ANO,然后利用“角边角”证明△AON和△COM全等,根据全等三角形对应边相等可得AN=CM,ON=OM,得出梯形ABMN和梯形CDNM关于点O对称,即可得出结论;
(2)根据翻折的性质,MN与AC互相垂直时点C与A重合;
(3)连接AM,根据翻折的性质可得AM=MC,AD′=CD,∠AMN=∠CMN,再根据两直线平行,内错角相等可得∠ANM=∠CMN,然后求出∠AMN=∠ANM,根据等角对等边可得AM=AN,利用“HL”证明△ABM和△AD′N全等,根据全等三角形的面积相等可得S△AD′N=S△ABM,再根据三角形的面积求出BM=$\frac{1}{2}$AN,然后求解即可.
解答 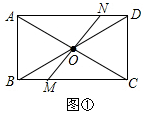 (1)证明:如图①,
(1)证明:如图①,
∵O为对角线的交点,
∴AO=CO,OB=OD,AD∥BC,
∵矩形ABCD的边AD∥BC,
∴∠MCO=∠ANO,
在△AON和△COM中,$\left\{\begin{array}{l}{∠MCO=∠ANO}&{\;}\\{AO=CO}&{\;}\\{∠AON=∠COM}&{\;}\end{array}\right.$,
∴△AON≌△COM(ASA),
∴AN=CM,ON=OM,
∴梯形ABMN和梯形CDNM关于点O对称,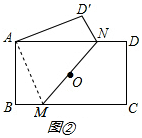
∴梯形ABMN≌梯形CDNM,
∴梯形ABMN的面积等于梯形CDNM的面积;
(2)解:当MN满足MN⊥AC时,才能使得点C恰好与点A重合.
(3)解:如图,连接AM,
∵矩形ABCD沿MN折叠,点C与点A重合,
∴AM=MC,AD′=CD,∠AMN=∠CMN,
∵AD∥BC,
∴∠ANM=∠CMN,
∴∠AMN=∠ANM,
∴AM=AN,
在△ABM和△AD′N中,$\left\{\begin{array}{l}{AM=AN}\\{AB=AD'}\end{array}\right.$,
∴△ABM≌△AD′N(HL),
∴S△AD′N=S△ABM,
∵翻折后不重叠部分的面积是重叠部分的面积的$\frac{1}{2}$,
∴$\frac{1}{2}$AB•BM=$\frac{1}{2}$×$\frac{1}{2}$AN•AB,
∴BM=$\frac{1}{2}$AN,
∵AM=MC=AN,
∴BM:MC=1:4,
∴MC=4BM.
点评 本题是四边形综合题目,考查了翻折变换的性质,全等三角形的判定与性质,矩形的性质,等角对等边的性质,以及平行线的性质,熟记翻折前后的两个图形能够完全重合得到相等的边和角是解题的关键.

| A. | 2.3×105 | B. | 3.2×105 | C. | 2.3×106 | D. | 5×106 |
| A. | (-2)2和-22 | B. | (-2)2和22 | C. | (-1)3和-1 | D. | |(-1)3|和|(-1)2| |
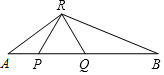 △PQR为等边三角形,∠ARB=120°
△PQR为等边三角形,∠ARB=120°