题目内容

19．如图，《九章算术》中国有下列问题解读“今有直角三角形，勾（短直角边）长为8步，股（长直角边）长为15步，问该直角三角形能容纳的圆（内切圆）直径是多少？”（　　）
A．3步B．5步C．6步D．8步

分析 根据勾股定理求出直角三角形的斜边，根据直角三角形的内切圆的半径的求法确定出内切圆半径，得到直径．

解答 解：根据勾股定理得：斜边=$\sqrt{{8}^{2}+1{5}^{2}}$=17，
∴内切圆直径=8+15-17=6（步），
故选：C．

点评 此题考查了三角形的内切圆与内心，掌握Rt△ABC中，两直角边分别为为a、b，斜边为c，其内切圆半径r=$\frac{a+b-c}{2}$是解题的关键．

练习册系列答案
相关题目
9．先阅读下列解法，再解答后面的问题．
已知$\frac{3x-4}{{x}^{2}-3x+2}$=$\frac{A}{x-1}$+$\frac{B}{x-2}$，求A、B的值．
解法一：将等号右边通分，再去分母，得：3x-4=A（x-2）+B（x-1），
即：3x-4=（A+B）x-（2A+B），
∴$\left\{\begin{array}{l}A+B=3\\-（2A+B）=-4\end{array}\right.$．
解得      $\left\{\begin{array}{l}A=1\\ B=2\end{array}\right.$．
解法二：在已知等式中取x=0，有-A+$\frac{B}{-2}$=-2，整理得
2A+B=4；
取x=3，有$\frac{A}{2}$+B=$\frac{5}{2}$，整理得
A+2B=5．
解    $\left\{\begin{array}{l}2A+B=4\\ A+2B=5\end{array}\right.$，
得：$\left\{\begin{array}{l}A=1\\ B=2\end{array}\right.$．
（1）已知$\frac{11x}{{-3{x^2}-14x+24}}=\frac{A}{x+6}+\frac{B}{4-3x}$，用上面的解法一或解法二求A、B的值．
（2）计算：
[$\frac{1}{{（x-1）（{x+1}）}}+\frac{1}{（x+1）（x+3）}+\frac{1}{（x+3）（x+5）}+…+\frac{1}{（x+9）（x+11）}$]（x+11），并求x取何整数时，这个式子的值为正整数．
10．正比例函数y=x与反比例函数y=$\frac{1}{x}$的图象相交于A，C两点，AB⊥x轴于B，CD⊥x轴于D，则四边形ABCD的面积为2．
7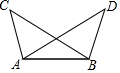．如图，已知△ABC≌△BAD，∠ABC=35°，则∠BAD=（　　）
A．30°B．35°C．60°D．70°
14．二次函数y=x2的图象向下平移2个单位后得到函数解析式为（　　）
A．y=x2+2B．y=x2-2C．y=（x-2）2D．y=（x+2）2
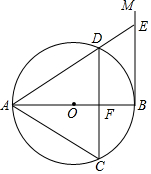4．如图，AB是⊙O的直径，过点B作⊙O的切线BM，弦CD∥BM，交AB于点F，且$\widehat{DA}$=$\widehat{DC}$，连接AC，AD，延长AD交BM于点E．
（1）求证：△ACD是等边三角形；
（2）连接OE，若⊙O的半径为2，求OE的值．
11．下列各式中，不相等的是（　　）
A．（-2）2和-22B．（-2）2和22C．（-1）3和-1D．|（-1）3|和|（-1）2|
8．用“＜”号把下列各数连接起来．
-4$\frac{1}{2}$，-（-$\frac{2}{3}$），|-0.6|，-0.6，-|-4.2|
9．2016年3月26日，由河北省游泳跳水运动管理中心主办的2016年河北省青少年游泳分站赛在唐山绿洲水上乐园举行，来自保定、秦皇岛灯地区的运动员达440名．在女子4×100米自由泳的比赛中，某教练记录了8组参赛选手的成绩，以240秒为标准，超出的记为正数，不足的记为负数，记录结果如下：
-13，+2，-8，-15，+3，-9，-5，+5
（1）这8组参赛选手中，成绩最好的是第几组？
（2）求这8组参赛选手的平均成绩．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网