题目内容
 如图,在△ABC中,∠B=60°,AB=2,BC=1+
如图,在△ABC中,∠B=60°,AB=2,BC=1+| 3 |
考点:解直角三角形
专题:计算题
分析:作AH⊥BC,如图,在Rt△ABH中,先利用余弦的定义可得到BH=2cos60°=1,再根据勾股定理计算出AH=
,易得CH=BC-BH=
,然后在Rt△ACH中,利用正切的定义计算出tanC=
=1,则根据特殊角的三角函数值即可得到∠ACB的度数.
| 3 |
| 3 |
| AH |
| CH |
解答:解:作AH⊥BC,如图,
在Rt△ABH中,∵cos∠B=
,
∴BH=2cos60°=1,
∴AH=
=
,
∵BC=1+
,
∴CH=BC-BH=1+
-1=
,
在Rt△ACH中,∵tanC=
=
=1,
∴∠C=45°.
故答案为45°.

在Rt△ABH中,∵cos∠B=
| BH |
| AB |
∴BH=2cos60°=1,
∴AH=
| AB2-BH2 |
| 3 |
∵BC=1+
| 3 |
∴CH=BC-BH=1+
| 3 |
| 3 |
在Rt△ACH中,∵tanC=
| AH |
| CH |
| ||
|
∴∠C=45°.
故答案为45°.
点评:本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.作BC边上的高是解决此题的关键.

练习册系列答案
相关题目
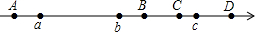 如图,有数数a、b、c在数轴上表示的点,如果|a|>|c|>|b|,那么数轴上的原点0可能是( )
如图,有数数a、b、c在数轴上表示的点,如果|a|>|c|>|b|,那么数轴上的原点0可能是( )| A、在A的位置 |
| B、在B的位置 |
| C、在C的位置 |
| D、在D的位置 |
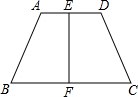 如图,在梯形ABCD中,AD∥BC,E、F分别是AD、BC的中点,且EF⊥BC,梯形ABCD是等腰梯形吗?
如图,在梯形ABCD中,AD∥BC,E、F分别是AD、BC的中点,且EF⊥BC,梯形ABCD是等腰梯形吗?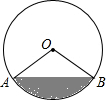 如图,有一个马戏帐篷,它的底面是圆形,其半径为20米.从A到B有一笔直的栅栏,其长为
如图,有一个马戏帐篷,它的底面是圆形,其半径为20米.从A到B有一笔直的栅栏,其长为 如图,直线AB、CD相交于点O,∠BOD与∠BOE互为余角,∠BOE=18°,则∠AOC=
如图,直线AB、CD相交于点O,∠BOD与∠BOE互为余角,∠BOE=18°,则∠AOC= 如图,已知BD是∠ABC的角平分线,DE⊥AB于E点,AB=6cm,BC=4cm,S△ABC=10cm2,则DE=
如图,已知BD是∠ABC的角平分线,DE⊥AB于E点,AB=6cm,BC=4cm,S△ABC=10cm2,则DE=