题目内容
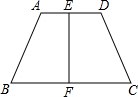 如图,在梯形ABCD中,AD∥BC,E、F分别是AD、BC的中点,且EF⊥BC,梯形ABCD是等腰梯形吗?
如图,在梯形ABCD中,AD∥BC,E、F分别是AD、BC的中点,且EF⊥BC,梯形ABCD是等腰梯形吗?考点:等腰梯形的判定
专题:
分析:过E作EM∥AB交BC于M,作EN∥CD交BC于N,得出四边形ABME和四边形ENCD是平行四边形,根据平行四边形的性质得出AB=EM,CD=EN,AE=BM,DE=CN,求出FM=FN,证△EFM≌△EFN,推出EM=EN,求出AB=CD即可.
解答:解:四边形ABCD是等腰梯形,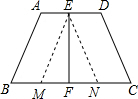
理由是:过E作EM∥AB交BC于M,作EN∥CD交BC于N,
∵AD∥BC,
∴四边形ABME和四边形ENCD是平行四边形,
∴AB=EM,CD=EN,AE=BM,DE=CN,
∵E、F分别是AD、BC的中点,
∴AE=DE,BF=CF,
∴FM=FN,
∵EF⊥BC,
∴∠EFM=∠EFN=90°,
在△EFM和△EFN中
∴△EFM≌△EFN(SAS),
∴EM=EN,
∵AB=EM,CD=EN,
∴AB=CD,
∵四边形ABCD是梯形,
∴四边形ABCD是等腰梯形.

理由是:过E作EM∥AB交BC于M,作EN∥CD交BC于N,
∵AD∥BC,
∴四边形ABME和四边形ENCD是平行四边形,
∴AB=EM,CD=EN,AE=BM,DE=CN,
∵E、F分别是AD、BC的中点,
∴AE=DE,BF=CF,
∴FM=FN,
∵EF⊥BC,
∴∠EFM=∠EFN=90°,
在△EFM和△EFN中
|
∴△EFM≌△EFN(SAS),
∴EM=EN,
∵AB=EM,CD=EN,
∴AB=CD,
∵四边形ABCD是梯形,
∴四边形ABCD是等腰梯形.
点评:本题考查了平行四边形的性质和判定,等腰梯形的判定,全等三角形的性质和判定的应用,解此题的关键是能正确作出辅助线,并进一步推出AB=CD,注意:两腰相等的梯形是等腰梯形.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
甲站到乙站另有8个中间停靠站,共需准备( )种动车票.
| A、90 | B、56 | C、45 | D、28 |
半径为5的圆中,72°圆心角所对弧长为( )
| A、π | B、2π | C、4π | D、5π |
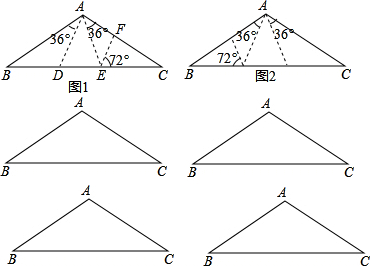 已知△ABC中AB=AC,∠BAC=108°,如图1,将它分割成四个非直角三角形,得其中的二个全等,二个相似(相似比不为1)请在以下四个图中设计不同的分割方法,将顶角为108°的等腰△ABC分割成四个非直角三角形,使得其中二个全等,另外二个相似(相似比不等于1),并在图上标注必要的角度,图1和图2被认为是同一种方法.
已知△ABC中AB=AC,∠BAC=108°,如图1,将它分割成四个非直角三角形,得其中的二个全等,二个相似(相似比不为1)请在以下四个图中设计不同的分割方法,将顶角为108°的等腰△ABC分割成四个非直角三角形,使得其中二个全等,另外二个相似(相似比不等于1),并在图上标注必要的角度,图1和图2被认为是同一种方法. 如图,已知线段AB,请用尺规按下列要求作图.
如图,已知线段AB,请用尺规按下列要求作图. 如图,在△ABC中,∠B=60°,AB=2,BC=1+
如图,在△ABC中,∠B=60°,AB=2,BC=1+ 根据正弦函数的定义你能得出锐角正弦值的取值范围吗?
根据正弦函数的定义你能得出锐角正弦值的取值范围吗?