题目内容
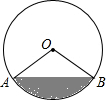 如图,有一个马戏帐篷,它的底面是圆形,其半径为20米.从A到B有一笔直的栅栏,其长为20
如图,有一个马戏帐篷,它的底面是圆形,其半径为20米.从A到B有一笔直的栅栏,其长为20| 3 |
考点:垂径定理的应用,勾股定理
专题:
分析:过C作CD⊥AB,D为垂足,则AD=BD=10
,根据cosA=
=
=
,得到∠A=30°,所以∠ACB=180°-30°-30°=120°,由S阴影部分=S扇形CAB-S△CAB=
-
×20
×10≈245.5m2,然后乘以3即可得到该校看马戏的人数.
| 3 |
| AD |
| AC |
10
| ||
| 20 |
| ||
| 2 |
| 120π×202 |
| 360 |
| 1 |
| 2 |
| 3 |
解答: 解:过C作CD⊥AB,D为垂足,
解:过C作CD⊥AB,D为垂足,
∵AB=20
米.
∴AD=BD=10
,
∵cosA=
=
=
,
∴∠A=30°,
∴∠ACB=180°-30°-30°=120°,
∴S阴影部分=S扇形CAB-S△CAB=
-
×20
×10≈245.5m2,
∴245.5×3≈756(人).
答:大约有736位观众在看马戏.
 解:过C作CD⊥AB,D为垂足,
解:过C作CD⊥AB,D为垂足,∵AB=20
| 3 |
∴AD=BD=10
| 3 |
∵cosA=
| AD |
| AC |
10
| ||
| 20 |
| ||
| 2 |
∴∠A=30°,
∴∠ACB=180°-30°-30°=120°,
∴S阴影部分=S扇形CAB-S△CAB=
| 120π×202 |
| 360 |
| 1 |
| 2 |
| 3 |
∴245.5×3≈756(人).
答:大约有736位观众在看马戏.
点评:本题考查的是垂径定理的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
x=-2是下列( )方程的解.
| A、5x+7=7-2x | ||
| B、6x-8=8x-4 | ||
| C、3x-2=4+x | ||
D、
|
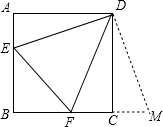 正方形ABCD的边长为6,E,F分别是AB,BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.
正方形ABCD的边长为6,E,F分别是AB,BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM. 已知:如图,A,B,C在同一条线段上,M是线段AC的中点,N是线段BC的中点,且AM=5cm,CN=3cm,则线段AB的长为
已知:如图,A,B,C在同一条线段上,M是线段AC的中点,N是线段BC的中点,且AM=5cm,CN=3cm,则线段AB的长为 如图,在△ABC中,∠B=60°,AB=2,BC=1+
如图,在△ABC中,∠B=60°,AB=2,BC=1+