题目内容
6.观察下列各正方形图案,每条边上有n(n≥2)个圆点,每个图案中圆点的总数是s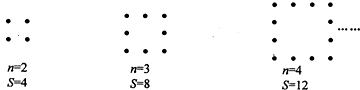
按此规律推断出:n=5,s=16.n与s的关系为S=4n-4.
分析 首先找到每条边上的圆点的个数的规律,然后计算四个边上的和即可.
解答 解:当n=2时,圆点的总个数为:S=2×4-4=4;
当n=3时,圆点的总个数为:S=3×4-4=8;
当n=4时,圆点的总个数为:S=4×4-4=12;
当n=5时,圆点的总个数为:S=5×4-4=16;
…
当n=n时,圆点的总个数为:S=4n-4;
故答案为:16,4n-4.
点评 本题考查了图形的变化类问题,解题的关键是能够找到边的变化规律,从而找到总数的规律,难度不大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.下列各组的两个数中,运算后结果相等的是( )
| A. | 23和 32 | B. | -33和 (-3)3 | C. | -22和(-2)2 | D. | -|-2|和-(-2) |
11.在“母亲节”期间,某校部分团员参加社会公益活动,准备构建一批许愿瓶进行销售,并将所得利润捐给慈善机构,根据市场调查,这种许愿瓶一段时间内的销售量y(个)与销售单价x(元/个)之间的对应关系如表所示:
(1)试判断y与x之间的函数关系,并求出函数关系式;
(2)若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润w(元)与销售单价x(元/个)之间的函数关系式;为了方便顾客,售价定位多少时可获利1200元;
(3)若许愿瓶的进货成本不超过900元,要想获得最大利润,试确定此时的销售单价,并求出此时的最大利润.
(1)试判断y与x之间的函数关系,并求出函数关系式;
(2)若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润w(元)与销售单价x(元/个)之间的函数关系式;为了方便顾客,售价定位多少时可获利1200元;
(3)若许愿瓶的进货成本不超过900元,要想获得最大利润,试确定此时的销售单价,并求出此时的最大利润.
| z(元/个) | 16 | 14 | 12 | 10 |
| y(个) | 120 | 180 | 240 | 300 |
15.一个直角三角形的两条直角边相差5cm,面积是7cm2,斜边长是( )
| A. | $\sqrt{14}$ | B. | $\sqrt{35}$ | C. | $\sqrt{53}$ | D. | $\sqrt{74}$ |
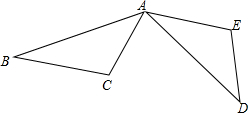 如图,△ABC按逆时针方向旋转得到△ADE
如图,△ABC按逆时针方向旋转得到△ADE