题目内容
函数y=x2-3x+4的图象与坐标轴的交点个数是( )
| A、0个 | B、1个 | C、2个 | D、3个 |
考点:抛物线与x轴的交点
专题:
分析:①当y=0时,△<0,所以抛物线y=x2-3x+4与x轴没有交点,②当x=0时,y=4,可求得抛物线与y轴交点,即可解题.
解答:解:①当y=0时,解方程x2-3x+4=0,
∵△=b2-4ac=9-16=-7<0,
∴方程无解,
∴抛物线数y=x2-3x+4的图象与x轴没有交点,
②∵当x=0时,y=4,
∴抛物线数y=x2-3x+4的图象与y轴交点为(0,4),
故抛物线数y=x2-3x+4的图象与坐标轴交点为1个.
故选 B.
∵△=b2-4ac=9-16=-7<0,
∴方程无解,
∴抛物线数y=x2-3x+4的图象与x轴没有交点,
②∵当x=0时,y=4,
∴抛物线数y=x2-3x+4的图象与y轴交点为(0,4),
故抛物线数y=x2-3x+4的图象与坐标轴交点为1个.
故选 B.
点评:本题考查了抛物线与坐标轴的交点的求解,本题考点为:当△>0时,抛物线与x轴有2个交点,当△<0时,抛物线与x轴没有交点,当△=0时,抛物线与x轴有一个交点.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
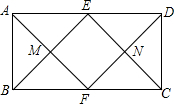 如图,在矩形ABCD中,E,F分别是AD,BC中点,连接AF,BE,CE,DF分别交于点M,N,四边形EMFN是( )
如图,在矩形ABCD中,E,F分别是AD,BC中点,连接AF,BE,CE,DF分别交于点M,N,四边形EMFN是( )| A、正方形 | B、菱形 |
| C、矩形 | D、无法确定 |
下列说法错误的个数是( )
①无理数都是无限小数;
②
的平方根是±2;
③
=(
)2;
④与数轴上的点一一对应的数是实数.
①无理数都是无限小数;
②
| (-2)2 |
③
| a2 |
| a |
④与数轴上的点一一对应的数是实数.
| A、1个 | B、2个 | C、3个 | D、4个 |
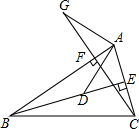 如图,BE,CF分别是△ABC的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AG,AD.求证:
如图,BE,CF分别是△ABC的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AG,AD.求证: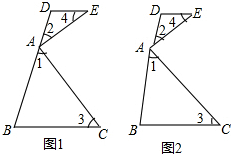 如图,∠EAC=90°,∠1+∠2=90°,∠1=∠3.∠2=∠4.
如图,∠EAC=90°,∠1+∠2=90°,∠1=∠3.∠2=∠4.
 某校体育老师为了解该校八年级学生对球类运动项目的喜爱情况,进行了随机抽样调查(每位学生必须且只能选择一项最喜爱的运动项目),并将调查结果进行整理,绘制了如图不完整的统计图表.请根据图表中的信息解答下列问题:
某校体育老师为了解该校八年级学生对球类运动项目的喜爱情况,进行了随机抽样调查(每位学生必须且只能选择一项最喜爱的运动项目),并将调查结果进行整理,绘制了如图不完整的统计图表.请根据图表中的信息解答下列问题: