题目内容
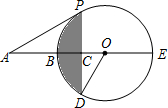 如图,BE是⊙O的直径,点A在EB的延长线上,弦PD⊥BE,垂足为C,连接OD,∠AOD=∠APC.
如图,BE是⊙O的直径,点A在EB的延长线上,弦PD⊥BE,垂足为C,连接OD,∠AOD=∠APC.(1)求证:AP是⊙O的切线.
(2)若⊙O的半径是4,AP=4
| 3 |
考点:切线的判定,扇形面积的计算
专题:计算题
分析:(1)连接OP,如图,利用等腰三角形的性质由OD=OP得到∠OPD=∠ODP,而∠APC=∠AOD,则∠OPD+∠APC=∠ODP+∠AOD,由于∠ODP+∠AOD=90°,易得∠APO=90°,于是根据切线的判定定理即可得到AP是⊙O的切线;
(2)在Rt△APO中,利用勾股定理计算出,AO=8,即PO=
AO,则∠A=30°,可计算出∠POA=60°,∠OPC=30°,再利用垂径定理PC=CD,且∠POD=120°,OC=
PO=2,接着在Rt△OPC中计算出PC=2
,得到PD=2PC=4
,然后根据扇形面积公式和S阴影=S扇形OPBD-S△OPD进行计算即可.
(2)在Rt△APO中,利用勾股定理计算出,AO=8,即PO=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
解答: (1)证明:连接OP,如图,
(1)证明:连接OP,如图,
∵OD=OP,
∴∠OPD=∠ODP,
∵∠APC=∠AOD,
∴∠OPD+∠APC=∠ODP+∠AOD,
又∵PD⊥BE,
∴∠ODP+∠AOD=90°,
∴∠OPD+∠APC=90°,
即∠APO=90°,
∴OP⊥AP,
∴AP是⊙O的切线;
(2)解:在Rt△APO中,
∵AP=4
,PO=4,
∴AO=
=8,即PO=
AO,
∴∠A=30°,
∴∠POA=60°,
∴∠OPC=30°
又∵PD⊥BE,
∴PC=CD,
∴∠POD=120°,OC=
PO=2,
在Rt△OPC中,∵OC=2,OP=4,
∴PC=
=2
,
∴PD=2PC=4
,
∴S阴影=S扇形OPBD-S△OPD
=
•π•42-
×4
×2
=
π-4
.
 (1)证明:连接OP,如图,
(1)证明:连接OP,如图,∵OD=OP,
∴∠OPD=∠ODP,
∵∠APC=∠AOD,
∴∠OPD+∠APC=∠ODP+∠AOD,
又∵PD⊥BE,
∴∠ODP+∠AOD=90°,
∴∠OPD+∠APC=90°,
即∠APO=90°,
∴OP⊥AP,
∴AP是⊙O的切线;
(2)解:在Rt△APO中,
∵AP=4
| 3 |
∴AO=
| AP2+PO2 |
| 1 |
| 2 |
∴∠A=30°,
∴∠POA=60°,
∴∠OPC=30°
又∵PD⊥BE,
∴PC=CD,
∴∠POD=120°,OC=
| 1 |
| 2 |
在Rt△OPC中,∵OC=2,OP=4,
∴PC=
| OP2-OC2 |
| 3 |
∴PD=2PC=4
| 3 |
∴S阴影=S扇形OPBD-S△OPD
=
| 120 |
| 360 |
| 1 |
| 2 |
| 3 |
=
| 16 |
| 3 |
| 3 |
点评:本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.在判定一条直线为圆的切线时,当已知条件中未明确指出直线和圆是否有公共点时,常过圆心作该直线的垂线段,证明该线段的长等于半径;当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线.也考查了垂径定理和扇形的面积公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在2,-2,0,-
四个数中,最小的数是( )
| 1 |
| 2 |
| A、2 | ||
| B、-2 | ||
| C、0 | ||
D、-
|
 如图,桌面上有木条b、c固定,木条a在桌面上绕点O旋转n°(0<n<90)后与b平行,则n=( )
如图,桌面上有木条b、c固定,木条a在桌面上绕点O旋转n°(0<n<90)后与b平行,则n=( )| A、20 | B、30 | C、70 | D、80 |
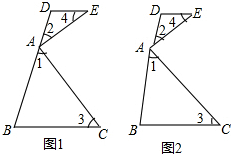 如图,∠EAC=90°,∠1+∠2=90°,∠1=∠3.∠2=∠4.
如图,∠EAC=90°,∠1+∠2=90°,∠1=∠3.∠2=∠4.
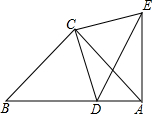 如图,等腰Rt△ACB中,∠ACB=90°,AC=BC,AB=9,D为AB上一点,AD=3,连接CD,以CD为边等腰Rt△ECD,使∠ECD=90°,EC=CD,连接AE.
如图,等腰Rt△ACB中,∠ACB=90°,AC=BC,AB=9,D为AB上一点,AD=3,连接CD,以CD为边等腰Rt△ECD,使∠ECD=90°,EC=CD,连接AE. 某校体育老师为了解该校八年级学生对球类运动项目的喜爱情况,进行了随机抽样调查(每位学生必须且只能选择一项最喜爱的运动项目),并将调查结果进行整理,绘制了如图不完整的统计图表.请根据图表中的信息解答下列问题:
某校体育老师为了解该校八年级学生对球类运动项目的喜爱情况,进行了随机抽样调查(每位学生必须且只能选择一项最喜爱的运动项目),并将调查结果进行整理,绘制了如图不完整的统计图表.请根据图表中的信息解答下列问题: 如图,a∥b,∠ABC=50°,若△ABC是等腰三角形,则∠α=
如图,a∥b,∠ABC=50°,若△ABC是等腰三角形,则∠α=