题目内容
6．
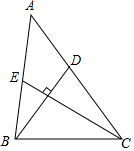如图，在△ABC中，BD，CE分别为AC，AB边上的中线，BD⊥CE，若BD=4，CE=6，则△ABC的面积为（ ）| A． | 12 | B． | 24 | C． | 16 | D． | 32 |
分析 根据题意得到点O是△ABC的重心，得到OC=$\frac{2}{3}$CE=4，根据三角形的面积公式求△BDC的面积，根据三角形的中线的性质计算即可．
解答 
解：∵BD，CE分别为AC，AB边上的中线，
∴点O是△ABC的重心，
∴OC=$\frac{2}{3}$CE=4，
∴△BDC的面积=$\frac{1}{2}$×BD×OC=8，
∵BD为AC边上的中线，
∴△ABC的面积=2×△BDC的面积=16，
故选：C．
点评 本题考查的是重心的概念和性质：三角形的重心是三角形三条中线的交点，且重心到顶点的距离是它到对边中点的距离的2倍．
练习册系列答案
智慧小复习系列答案
相关题目
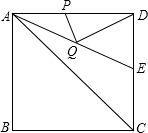如图，正方形ABCD的边长为4，∠DAC的平分线交DC于点E，若点P、Q分别是AD和AE上的动点，则DQ+PQ的最小值是2$\sqrt{2}$．
如图，直线y=x与直线y=2x-1相交于点B，过B作BA⊥y轴于点A，点A关于点B的对称点为A1，过A1作A2A3∥y轴交直线l2于点A2，过A2作A2A3∥x轴交直线l1于点A3，…，按这个方式操作，则线段A15A16的长为（ ）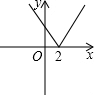
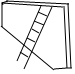（1）如图，长3m的梯子斜靠着墙，梯子底端离墙底0.6m，问梯子顶端离地面多少米？（精确到0.1m）