题目内容
暑假将至，某商场为了吸引顾客，设计了可以自由转动的转盘（如图所示，转盘被均匀地分为20份），并规定：顾客每 200元的商品，就能获得一次转动转盘的机会．如果转盘停止后，指针正好对准红色、黄色、绿色区域，那么顾客就可以分别获得200元、100元、50元的购物券，凭购物券可以在该商场继续购物．若某顾客购物300元．
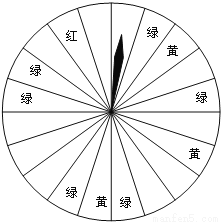
（1）求他此时获得购物券的概率是多少？
（2）他获得哪种购物券的概率最大？请说明理由．
（1）；（2）获得50元购物券的概率最大．
【解析】
试题分析：（1）由转盘被均匀地分为20份，他此时获得购物券的有10份，直接利用概率公式求解即可求得答案；
（2）分别求得获得200元、100元、50元的购物券的概率，即可求得答案．
【解析】
（1）∵转盘被均匀地分为20份，他此时获得购物券的有10份，
∴他此时获得购物券的概率是：=；
（2）∵P（获得20...
练习册系列答案
相关题目
如图，某水库堤坝横断面迎水坡AB的坡比是1: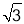
，堤坝高BC=50m，则迎水坡面AB的长度是（ ）.
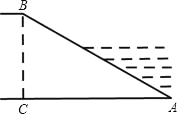
A．100m B．100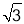m C．150m D．50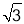m
A．
【解析】
试题分析：根据题意可得，把BC=50m，代入即可算出AC的长，再利用勾股定理算出AB的长即可．∵堤坝横断面迎水坡AB的坡比是1: ，∴，∵BC=50m，∴AC=50m，∴AB==100m，故选：A． 如图，ΔABC≌ΔDEF，∠A=25°，∠B=65°，BF=3㎝，求∠DFE的度数和EC的长.
∠DFE=65°；EC=3㎝.
【解析】根据已知条件，△ABC≌△DEF，可知∠E=∠B=65°，BF=BC，可证EC=BF=3cm，做题时要正确找出对应边，对应角．
△ABC中∠A=25°，∠B=65°，
∴∠BCA=180°-∠A-∠B=180°-25°-65°=90°，
∵△ABC≌△DEF，
∴∠BCA=∠DFE，BC=EF，
∴EC=BF=3cm，
... 下列图中，与左图中的图案完全一致的是（）
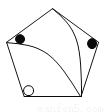
A.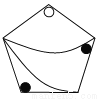 
B.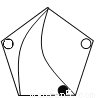 
C.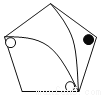 
D.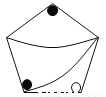 
A
【解析】A图案可以通过旋转得到，故A符合题意；B、C、D通过旋转、平移都不能得到，
故选A. 在下列各组图形中，是全等的图形是（）
C
【解析】试题分析：能够完全重合的两个图形叫做全等形．只有选项C能够完全重合，A中大小不一致，B，D中形状不同．
【解析】
由全等形的概念可以判断：C中图形完全相同，符合全等形的要求，而A、B、D中图形很明显不相同，A中大小不一致，B，D中形状不同．
故选C． 从分别标有1、2、3、4的四张卡片中，一次同时抽2张，其中和为奇数的概率是 ．
【解析】试题分析：如图所示，
由树状图可知共有4×3=12种可能，和为奇数的有8种，所以概率是＝．故答案为： ． 在相同条件下重复试验，若事件A发生的概率是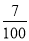
，下列陈述中，正确的是（ ）
A. 事件A发生的频率是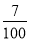
B. 反复大量做这种试验，事件A只发生了7次
C. 做100次这种试验，事件A一定发生7次
D. 做100次这种试验，事件A可能发生7次
D
【解析】试题分析：∵事件A发生的概率是，不表示事件A发生的频率是，
∴选项A不正确；∵事件A发生的概率是，不表示事件A只发生了7次，可能比7次多，也有可能比7次少，
∴选项B不正确；
∵事件A发生的概率是，不表示事件A一定发生7次，
∴选项C不正确；
∵事件A发生的概率是，表示事件A可能发生7次，
∴选项D正确．
故选D． 如图，为测量B点到河对面的目标A之间的距离，他们在B点同侧选择了一点C，测得∠ABC＝70°，∠ACB＝40°，然后在M处立了标杆，使∠CBM＝70°，∠BCM＝40°，那么需要测量________才能测得A，B之间的距离( )
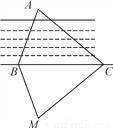
A. AB B. AC C. BM D. CM
C
【解析】∵∠ABC=∠CBM=70°，BC=BC，∠ACB=∠MCB=40°，
∴△ABC≌△MBC，∴AB=BM，
所以需要测量BM的长才能测得A、B之间的距离，
故选C. 如图，在四边形ABCD中，E、F分别是AB、AD的中点．若EF＝2，BC＝5，CD＝3，则cosC的值为_______．
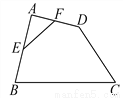
【解析】连接BD，
∵E、F分别是AB、AD的中点，
∴EF∥BD，且BD=2EF=4，
∵BD=4，BC=5，CD=3，
∴△BDC是直角三角形，
∴tan C=，
故答案为： .