题目内容
13. 如图,直角三角形ABC中,AC=4,BC=3,P为斜边AB上一动点,且PE⊥AC,PF⊥BC,垂足分别是E、F,则线段EF长度的最小值是$\frac{12}{5}$.
如图,直角三角形ABC中,AC=4,BC=3,P为斜边AB上一动点,且PE⊥AC,PF⊥BC,垂足分别是E、F,则线段EF长度的最小值是$\frac{12}{5}$.
分析 先由矩形的判定定理推知四边形PECF是矩形;连接PC,则PC=EF,所以要使EF,即PC最短,只需PC⊥AB即可;然后根据三角形的等积转换即可求得PC的值.
解答 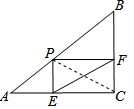 解:连接PC.
解:连接PC.
∵PE⊥AC,PF⊥BC,
∴∠PEC=∠PFC=∠C=90°;
又∵∠ACB=90°,
∴四边形ECFP是矩形,
∴EF=PC,
∴当PC最小时,EF也最小,
即当CP⊥AB时,PC最小,
∵AC=4,BC=3,
∴AB=5,
∴$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•PC,
∴PC=$\frac{12}{5}$.
∴线段EF长的最小值为$\frac{12}{5}$;
故答案为:$\frac{12}{5}$.
点评 本题考查了勾股定理、矩形的判定与性质、垂线段最短.利用“两点之间垂线段最短”找出PC⊥AB时,PC取最小值是解答此题的关键.

练习册系列答案
相关题目
4.下列图案是几种汽车的标志,这几个图案中是轴对称图形的共有( )


| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
2.若0<a<1,则不等式(x-a)(x-$\frac{1}{a}$)<0的解为( )
| A. | {x|a<x<$\frac{1}{a}$} | B. | {x|$\frac{1}{a}$<x<a} | C. | {x|x<a或x>$\frac{1}{a}$} | D. | {x|x<$\frac{1}{a}$或x>a} |
3.下列各式不能使用平方差公式的是( )
| A. | (2a+b)(2a-b) | B. | (-2a+b)(b-2a) | C. | (-2a+b)(-2a-b) | D. | (2a-b)-(2a-b) |
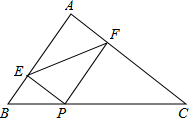 在△ABC中,AB=6cm,AC=8cm,BC=10cm,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,连接EF,则EF的最小值为$\frac{24}{5}$cm.
在△ABC中,AB=6cm,AC=8cm,BC=10cm,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,连接EF,则EF的最小值为$\frac{24}{5}$cm.